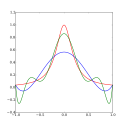
Rungeho jev

Rungeho jev je problém v numerické matematice, který objevil v roce 1901 německý matematik Carl Runge, když zkoumal chování chyb při aproximaci funkcí pomocí interpolačních polynomů na množině ekvidistantních interpolačních bodů.^[1] Runge zjistil, že použití polynomu vyššího stupně vždy nezlepšuje přesnost; naopak, na okrajích intervalu se objevují oscilace. Jev je podobný Gibbsově jevu při aproximaci Fourierovou řadou.

Úvod

Weierstrassova věta o aproximaci říká, že ke každé spojité funkci f(x) definované na uzavřeném intervalu ${\displaystyle \langle a,b\rangle }$ existuje posloupnost polynomiálních funkcí P_n(x) pro n=0, 1, 2, …, stupně nejvýše n, které aproximují funkci f(x), a na intervalu ${\displaystyle \langle a,b\rangle }$ k ní konvergují stejnoměrně, tj.

${\displaystyle \lim _{n\rightarrow \infty }\left(\max _{a\leq x\leq b}\left|f(x)-P_{n}(x)\right|\right)=0.}$

Chceme funkci f(x) interpolovat v n+1 ekvidistantních bodech polynomem P_n(x) n-tého stupně, který těmito body prochází, můžeme na základě Weierstrassovy věty očekávat, že při použití více bodů bude rekonstrukce funkce f(x) přesnější. Ale tato určitá množina polynomiálních funkcí P_n(x) nezaručuje stejnoměrnou konvergenci; věta pouze tvrdí, že taková sada polynomiálních funkcí existuje. Věta sama neříká, jak najít takovou posloupnost polynomů; k tomu je možné použít Bernsteinovy polynomy.

Řada funkcí P_n(x) vytvořená tímto způsobem může pro rostoucí n divergovat od f(x); typicky se to projeví výskytem oscilací, které se v blízkosti koncových interpolačních bodů zvětšují. Objev tohoto jevu je připisován Rungemu.^[2]

Problém

Uvažujme Rungeho funkci

${\displaystyle f(x)={\frac {1}{1+25x^{2}}}\,}$

(zvětšená verze Agnesiny křivky). Runge zjistil, že při interpolaci této funkce v ekvidistantních bodech x_i na intervalu −1 a 1 tak, že:

${\displaystyle x_{i}={\frac {2i}{n}}-1,\quad i\in \left\{0,1,\dots ,n\right\}}$

polynomy P_n(x) stupně nejvýše n, výsledná interpolační funkce kmitá na konci intervalu, tj. blízko k −1 a 1. Dokonce lze dokázat, že interpolační chyba se při zvyšování stupně polynomu zvětšuje (bez omezení):

${\displaystyle \lim _{n\rightarrow \infty }\left(\max _{-1\leq x\leq 1}|f(x)-P_{n}(x)|\right)=+\infty .}$

To ukazuje, že interpolace polynomem vysokého stupně v ekvidistantních bodech může být problematická.

Příčina

Rungeho jev je důsledkem dvou vlastností tohoto problému:

• Hodnota derivací n-tého řádu této funkce rychle roste se zvětšujícím se n.
• Ekvidistance mezi body vede k Lebesgueově konstantě, která rychle roste se zvětšujícím se n.

Jev je graficky dobře viditelný, protože obě vlastnosti se kombinují a zvyšují řád oscilace.

Chyba mezi vytvořující funkcí a interpolačním polynomem řádu n je

${\displaystyle f(x)-P_{n}(x)={\frac {f^{(n+1)}(\xi )}{(n+1)!}}\prod _{i=0}^{n}(x-x_{i})}$

pro nějaké ${\displaystyle \xi }$ z intervalu (−1, 1). Tedy

${\displaystyle \max _{-1\leq x\leq 1}|f(x)-P_{n}(x)|\leq \max _{-1\leq x\leq 1}{\frac {\left|f^{(n+1)}(x)\right|}{(n+1)!}}\max _{-1\leq x\leq 1}\prod _{i=0}^{n}|x-x_{i}|}$.

Označíme-li symbolem ${\displaystyle w_{n}(x)}$ nodální funkci

${\displaystyle w_{n}(x)=(x-x_{0})(x-x_{1})\cdots (x-x_{n})}$

a nechť ${\displaystyle W_{n}}$ je maximální řád funkce ${\displaystyle w_{n}}$:

${\displaystyle W_{n}=\max _{-1\leq x\leq 1}|w_{n}(x)|}$.

Je jednoduché dokázat, že pro ekvidistantní uzly

${\displaystyle W_{n}\leq n!h^{n+1}}$

kde ${\displaystyle h=2/n}$ je velikost kroku.

Pokud navíc předpokládáme, že (n+1)-tá derivace funkce ${\displaystyle f}$ je omezená:

${\displaystyle \max _{-1\leq x\leq 1}|f^{(n+1)}(x)|\leq M_{n+1}}$.

Proto

${\displaystyle \max _{-1\leq x\leq 1}|f(x)-P_{n}(x)|\leq M_{n+1}{\frac {h^{n+1}}{(n+1)}}}$.

Ale řád (n+1)-té derivace Rungeho funkce se zvyšuje s rostoucím n, protože ${\displaystyle M_{n+1}\leq (n+1)!5^{n+1}}$. Důsledkem je, že výsledná horní mez ${\displaystyle (10/n)^{n+1}n!}$ se blíží k nekonečnu, když n se blíží k nekonečnu.

Fakt, že horní mez chyby jde k nekonečnu, i když je často používán pro vysvětlení Rungeho jevu, samozřejmě neznamená, že samotná chyba také diverguje s rostoucím n.

Zmírňování problému

Změna interpolačních bodů

Oscilaci lze zmírnit použitím zahušťováním uzlů na okrajích intervalu. Například na intervalu ⟨−1,1⟩ lze použít body s asymptotickou hustotou danou vzorcem^[3] ${\displaystyle 1/{\sqrt {1-x^{2}}}}$. Standardním příkladem takové sady uzlů jsou Čebyševovy uzly, u nichž maximální chyba v aproximaci Rungeho funkce zaručeně klesá s rostoucím řádem polynomu. Jev ukazuje, že polynomy vysokého stupně jsou pro interpolaci s ekvidistantními uzly obecně nevhodné.

S-Rungeho algoritmus bez převzorkování

Když převzorkování^[ujasnit] na rozumné množině uzlů není proveditelné, je možné vyzkoušet S-Rungeho algoritmus.^[4] Při tomto přístupu je původní množina uzlů mapovaná na množinu Čebyševových uzlů, poskytujících stabilní polynomiální rekonstrukci. Zvláštností této metody je, že není potřeba převzorkování na mapovaných uzlech, které se také nazývají umělé uzly. Na github je implementace tohoto postupu v jazyce Python.

Aproximace polynomiální po částech

Popsanému problému se lze vyhnout použitím spline křivek, které jsou po částech polynomiální. Pro zmenšení interpolační chyby můžeme místo zvyšování stupně použitého polynomu zvyšovat počet polynomiálních částí, které se používají pro konstrukci spline křivky.

Omezená minimalizace

Můžeme také proložit polynom vyššího stupně (například pro ${\displaystyle n}$ bodů použít polynom řádu ${\displaystyle N=n^{2}}$ místo ${\displaystyle n+1}$) a použít takový interpolační polynom, jehož první (nebo druhá) derivace má minimální ${\displaystyle L^{2}}$ normu.

Podobným přístupem je minimalizace omezené verze vzdálenosti ${\displaystyle L^{p}}$ mezi m-tou derivací polynomu a střední hodnotou jeho m-té derivace. Explicitně pro minimalizaci

${\displaystyle V_{p}=\int _{a}^{b}\left|{\frac {\operatorname {d} ^{m}P_{N}(x)}{\operatorname {d} x^{m}}}-{\frac {1}{b-a}}\int _{a}^{b}{\frac {\operatorname {d} ^{m}P_{N}(z)}{\operatorname {d} z^{m}}}\operatorname {d} z\right|^{p}\operatorname {d} x-\sum _{i=1}^{n}\lambda _{i}\,\left(P_{N}(x_{i})-f(x_{i})\right),}$

kde ${\displaystyle N\geq n-1}$ a ${\displaystyle m<N}$, vzhledem ke koeficientům polynomu a Lagrangeovým multiplikátorům ${\displaystyle \lambda _{i}}$. Pro ${\displaystyle N=n-1}$ omezující rovnice generované Lagrangeovými multiplikátory omezují ${\displaystyle P_{N}(x)}$ na minimální polynom, který prochází všemi ${\displaystyle n}$ body. Na opačném konci ${\displaystyle \lim _{N\rightarrow \infty }P_{N}(x)}$ se bude blížit tvaru velmi podobnému po částech polynomiální aproximaci. Speciálně pro ${\displaystyle m=1}$ se ${\displaystyle \lim _{N\rightarrow \infty }P_{N}(x)}$ blíží po částech lineárním polynomům, tj. propojuje interpolační body úsečkami.

Při procesu minimalizace ${\displaystyle V_{p}}$ má ${\displaystyle p}$ za úkol omezovat velikost odchylek od střední hodnoty. Čím je ${\displaystyle p}$ větší, tím více jsou penalizovány větší odchylky v porovnání s malými. Hlavní výhodou Eukleidovské normy ${\displaystyle p=2}$ je, že umožňuje analytické řešení a zaručuje, že ${\displaystyle V_{p}}$ bude mít pouze jediné minimum. Pro ${\displaystyle p\neq 2}$ může ve ${\displaystyle V_{p}}$ existovat více minim, kvůli čemuž je obtížné zjistit, zda nalezené minimum je globálním minimem.

Použití metody nejmenších čtverců

Další metodou je proložení polynomu nižšího stupně použitím metody nejmenších čtverců. Obecně při použití ${\displaystyle m}$ ekvidistantních bodů, kde ${\displaystyle N<2{\sqrt {m}}}$ pak aproximace metodou nejmenších čtverců ${\displaystyle P_{N}(x)}$ je dobře podmíněná.^[5]

Bernsteinův polynom

Bernsteinovy polynomy umožňují stejnoměrně aproximovat každou spojitou funkci na uzavřeném intervalu. Tato metoda je však poněkud výpočetně náročná.^[zdroj?]

Příbuzná tvrzení z teorie aproximace

Pro každou předdefinovanou tabulku interpolačních uzlů existuje spojitá funkce, pro kterou posloupnost interpolační polynomů na těchto uzlech diverguje.^[6] Pro každou spojitou funkci existuje tabulka uzlů, na kterých interpolační proces konverguje.^[zdroj?] Čebyševova interpolace (na Čebyševových uzlech) konverguje stejnoměrně pro každou absolutně spojitou funkci.

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Runge's phenomenon na anglické Wikipedii.

Související články

• Srovnejte s Gibbsovým jevem pro sinusové bázové funkce
• Taylorova řada
• Čebyševovy uzly
• Stoneova–Weierstrassova věta