Schulzeho metoda
Schulzeho metoda je volební systém navržený v roce 1997 Markem Schulzem. Vytváří setříděný seznam vítězů, který bere v úvahu preference.
Její základní vlastností je, že dva kandidáti jsou v seznamu vždy setříděni stejným způsobem, jakým by volba dopadla, kdyby se rozhodovalo jen mezi nimi dvěma. Jedná se tedy o jednu z Condorcetových metod. Z nich je v současnosti nejpoužívanější, používají ji například organizace Nadace Wikimedia, Debian, Gentoo Linux a Software in the Public Interest.
Je více způsobů, jak spočítat výsledek Schulzeho metody. Všechny dávají stejný výsledek a liší se pouze v postupu.
Volba z hlediska voliče

V případě Schulzeho metody podobně jako v případě jiných preferenčních systémů je na každém hlasovacím lístku seznam všech kandidátů, které může volič seřadit podle pořadí, v jakém je preferuje. Obvykle se používá vzestupný systém, tedy číslo 1 napíše volič k tomu kandidátovi, kterého preferuje nejvíce, číslo 2 k druhému nejpreferovanějšímu a tak dále. Přitom platí, že volič smí:
- dát stejné číslo více kandidátům, aby dal najevo, že oba preferuje stejně
- nepřidělit některým kandidátům žádná čísla — to je interpretováno tak, že
- volič preferuje všechny kandidáty s přiděleným číslem před těmi bez čísla
- na pořadí neoznačených kandidátů mu nezáleží
Výpočet výsledků pomocí cest
Základní myšlenkou výpočtu výsledku pomocí cest je představa nepřímých porážek, neboli cest. Terminologie zde odpovídá teorii grafů, kdy jednotliví kandidáti představují vrcholy a výsledky jejich vzájemného porovnávání představují orientované cesty.
Pokud kandidát K(1) v přímém porovnání poráží kandidáta K(2) (tedy více voličů dává přednost K(1) před K(2) než naopak), kandidát K(2) poráží v přímém porovnání kandidáta K(3) a tímto způsobem dále až ke kandidátovi K(n-1), který v přímém porovnání poráží kandidáta K(n), pak je zde cesta od kandidáta K(1) ke kandidátovi K(n). Síla této cesty je dána jejím nejslabším článkem, tedy počtem preferujících u nejtěsnějšího vítězství.
Formálněji řečeno:
- označme d[V,W] počet voličů, kteří preferují kandidáta V před kandidátem W
- cesta je posloupnost kandidátů K(1), …, K(n), kteří splňují d[K(i),K(i+1)]>d[K(i+1),K(i)] pro všechna i od 1 do n-1.
- síla této cesty je minimum z hodnot d[K(i),K(i+1)] pro i probíhající od 1 do n-1.
Síla nejsilnější cesty od kandidáta A ke kandidátovi B je definována jako maximum sil všech cest od A k B.
Kandidát A nepřímo poráží kandidáta B, pokud buď
- síla nejsilnější cesty od A k B je větší než síla nejsilnější cesty od B k A
- existuje cesta od A k B a neexistuje cesta od B k A
Platí, že relace nepřímého poražení je tranzitivní. Tedy poráží-li nepřímo kandidát A kandidáta B a kandidát B kandidáta C, pak také kandidát A nepřímo poráží kandidáta C.
Příklad
Máme 5 kandidátů: A, B, C, D, E a 45 voličů. Preference jsou následující:
- 5 ACBED (tím je myšleno, že pět voličů volí pořadí A > C > B > E > D)
- 5 ADECB
- 8 BEDAC
- 3 CABED
- 7 CAEBD
- 2 CBADE
- 7 DCEBA
- 8 EBADC
- 5 ADECB
| d[*,A] | d[*,B] | d[*,C] | d[*,D] | d[*,E] | |
|---|---|---|---|---|---|
| d[A,*] | 20 | 26 | 30 | 22 | |
| d[B,*] | 25 | 16 | 33 | 18 | |
| d[C,*] | 19 | 29 | 17 | 24 | |
| d[D,*] | 15 | 12 | 28 | 14 | |
| d[E,*] | 23 | 27 | 21 | 31 |
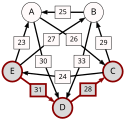
Nakreslená jako graf vypadá situace takto:

V následujícím grafu jsou červeně vyznačeny nejsilnější cesty od kandidáta X ke kandidátovi Y a jsou podtrženy nejslabší články, kterými je dána síla této nejsilnější cesty:
| p[*,A] | p[*,B] | p[*,C] | p[*,D] | p[*,E] | |
|---|---|---|---|---|---|
| p[A,*] | 28 | 28 | 30 | 24 | |
| p[B,*] | 25 | 28 | 33 | 24 | |
| p[C,*] | 25 | 29 | 29 | 24 | |
| p[D,*] | 25 | 28 | 28 | 24 | |
| p[E,*] | 25 | 28 | 28 | 31 |
Odtud vidíme, že vítězem bude kandidát E a celkové pořadí bude E > A > C > B > D, neboť:
Protože 25 = p[E,A] > p[A,E] = 24, kandidát E je lepší než kandidát A.
Protože 28 = p[E,B] > p[B,E] = 24, kandidát E je lepší než kandidát B.
Protože 28 = p[E,C] > p[C,E] = 24, kandidát E je lepší než kandidát C.
Protože 31 = p[E,D] > p[D,E] = 24, kandidát E je lepší než kandidát D.
Protože 28 = p[A,B] > p[B,A] = 25, kandidát A je lepší než kandidát B.
Protože 28 = p[A,C] > p[C,A] = 25, kandidát A je lepší než kandidát C.
Protože 30 = p[A,D] > p[D,A] = 25, kandidát A je lepší než kandidát D.
Protože 29 = p[C,B] > p[B,C] = 28, kandidát C je lepší než kandidát B.
Protože 29 = p[C,D] > p[D,C] = 28, kandidát C je lepší než kandidát D.
Protože 33 = p[B,D] > p[D,B] = 28, kandidát B je lepší než kandidát D.
Rozšíření
Tato metoda není v současnosti používána v žádných parlamentních volbách, ale postupně ji začínají používat některé organizace. Například ji používají následující organizace a projekty:
Odkazy
Reference
V tomto článku byl použit překlad textu z článku Schulze method na anglické Wikipedii.
Externí odkazy
 Obrázky, zvuky či videa k tématu Schulzeho metoda na Wikimedia Commons
Obrázky, zvuky či videa k tématu Schulzeho metoda na Wikimedia Commons
Média použitá na této stránce
Autor: Markus Schulze, Licence: CC BY-SA 3.0
Another graphic to illustrate the Schulze method.
Autor: Markus Schulze, Licence: CC BY-SA 3.0
Another graphic to illustrate the Schulze method.
Autor: Markus Schulze, Licence: CC BY-SA 3.0
Another graphic to illustrate the Schulze method.
Autor: Markus Schulze, Licence: CC BY-SA 3.0
Another graphic to illustrate the Schulze method.
Autor: Markus Schulze, Licence: CC BY-SA 3.0
Another graphic to illustrate the Schulze method.
Autor: Markus Schulze, Licence: CC BY-SA 3.0
Another graphic to illustrate the Schulze method.
Autor: Markus Schulze, Licence: CC BY-SA 3.0
Another graphic to illustrate the Schulze method.
Autor: Markus Schulze, Licence: CC BY-SA 3.0
Another graphic to illustrate the Schulze method.
Autor: Markus Schulze, Licence: CC BY-SA 3.0
Another graphic to illustrate the Schulze method.
Autor:
- Preferential_ballot.svg: Původně soubor načetl Rspeer na projektu Wikipedie v jazyce angličtina
Later version(s) were uploaded by Mark at en.wikipedia.
, Licence: CC BY-SA 3.0Created by en:User:Rspeer using en:Inkscape. Modified by Mark.
Autor: Markus Schulze, Licence: CC BY-SA 3.0
Another graphic to illustrate the Schulze method.
Autor: Markus Schulze, Licence: CC BY-SA 3.0
Another graphic to illustrate the Schulze method.
Autor: Markus Schulze, Licence: CC BY-SA 3.0
Another graphic to illustrate the Schulze method.
Autor: Markus Schulze, Licence: CC BY-SA 3.0
example to illustrate the Schulze method
Autor: Markus Schulze, Licence: CC BY-SA 4.0
Another graphic to illustrate the Schulze method.
Autor: Markus Schulze, Licence: CC BY-SA 3.0
Another graphic to illustrate the Schulze method.
Autor: Markus Schulze, Licence: CC BY-SA 3.0
Another graphic to illustrate the Schulze method.
Autor: Markus Schulze, Licence: CC BY-SA 3.0
Another graphic to illustrate the Schulze method.
Autor: Markus Schulze, Licence: CC BY-SA 3.0
Another graphic to illustrate the Schulze method.
Autor: Markus Schulze, Licence: CC BY-SA 3.0
Another graphic to illustrate the Schulze method.
Autor: Markus Schulze, Licence: CC BY-SA 3.0
Another graphic to illustrate the Schulze method.
Autor: Markus Schulze, Licence: CC BY-SA 3.0
Another graphic to illustrate the Schulze method.