Sedm základních nástrojů zlepšování kvality
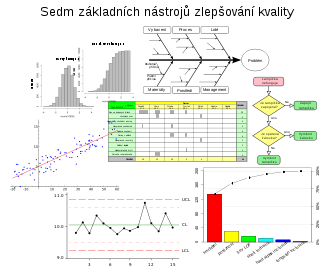
Sedm základních nástrojů na zlepšování kvality, Sedm základních nástrojů na zvyšování kvality nebo též Sedm základních nástrojů pro řízení jakosti (z anglického Seven Basic Tools of Quality), je pevně stanovený soubor především grafických technik napomáhajících řešení problémů s kvalitou. Mezi sedm základních nástrojů na zvyšování kvality patří diagram příčin a následků, kontrolní tabulka, histogram, Paretův diagram, korelační diagram, vývojový diagram a regulační diagram. Největšího využití nalezne těchto 7 nástrojů především v linkové výrobě, kde lze snadno sledovat zmetkovitost, případně chybovost jednotlivých strojů či zaměstnanců, ale i mimo tuto oblast. Jejich užití bývá ve firmách preferováno před složitějšími statistickými metodami pro svou jednoduchost.
Označení a jeho původ
Původní označení znělo původně pouze „Seven Tools“, tedy sedm nástrojů a jejich obsah byl zformován v průběhu padesátých a šedesátých let minulého století v Japonsku K. Išikawou a E. Demingem.[1][2]
Išikawa uvádí k celému významu následující:
- Soubor Sedmi základních nástrojů byl označen slovem „základní“ (anglicky basic), protože jsou dostatečně jednoduché na to, aby je mohl použít někdo s pouze základními znalostmi statistiky, přičemž je možné je použít na vyřešení téměř všech problémů spojených s kvalitou výroby.[3]
- Označení je inspirované slavným příběhem legendárního bojového mnicha Benkeiho a jeho sedmi zbraněmi, které s sebou neustále nosil, a které mu umožnily vyhrát všechny souboje.[4] Společnosti, které se v té době rozhodly vyškolit své pracovní síly v kontrole kvality zjistily, že celková složitost dohnala většinu zaměstnanců k osekání školení a používání jednodušších metod, které však přesto postačovaly na řešení většiny problémů spojených s kvalitou.[5]
Sedm základních nástrojů je v kontrastu s rozvinutějšími statistickými metodami, jako například výběrové šetření (survey sampling), náhodná kontrola (acceptance sampling), testování statistických hypotéz, plánování experimentů nebo multivariátní analýza a různými metodami vyvinutými v oblasti operační analýzy.[6]
Popis nástrojů
Mezi sedm základních nástrojů na zvyšování kvality patří:[7][8]
- Diagram příčin a následků, resp. Išikawův diagram, nazývaný též diagram rybí kosti (fishbone diagram)
- Kontrolní tabulka, též záznamník dat, sběr dat a třídění informací
- Histogram, rozdělení četnosti
- Paretův diagram (Pareto chart) nebo Paretova analýza
- Korelační diagram, též bodový graf (Scatter diagram), též regulační a korelační analýza
- Vývojový diagram (Flow chart)
- Regulační diagram (Control Chart)
Většina ze sedmi základních nástrojů představuje v podstatě kvantitativní metody, které přispívají k monitorování a lepšímu zvládnutí řízení procesu, lepšímu pochopení procesu včetně realizace procesního přístupu, lepší identifikaci, diagnostice a řešení problémů a k objektivnějšímu rozhodování a tím i k lepšímu fungování celého systému.[1]
Diagram příčin a následků

Diagram příčin a následků a též Išikawův diagram podle Kaoru Išikawy, který ho poprvé představil, nebo díky vzhledu také diagram rybí kosti (anglicky fishbone diagram), řeší úlohu určení pravděpodobné příčiny problému. Je používán pomocí brainstormingu, kdy jsou hledány všechny potenciální zdroje problému. Při sestavování diagramu tvoří problém tzv. hlavu rybí kosti a hlavní kosti vedoucí od páteře znamenají oblasti či kategorie, ve kterých se může problém nacházet. Vedlejší kosti pak znamenají konkrétní potenciální příčiny. Takto lze diagram vést ve více úrovních příčin a podpříčin, obvykle se však doporučuje použít nejvýše 2 úrovně.[9] Išikawův diagram se používá především na řešení situací, kdy tým inklinuje k myšlení „ve vyjetých kolejích“. Pro konstrukci diagramu je vhodné použít skupinové setkání. Nancy R. Tague uvádí následující postup:[7]
- Shodnout se na pojmenování problému, který tvoří „hlavu“ rybí kosti a nakreslit vodorovnou šipku k ní směřující.
- Provést brainstorming ohledně hlavních příčin tohoto problému. Pokud je to obtížné, je možné použít obecné příčiny z daného odvětví, např. postupy, stroje (zařízení), lidé (pracovní síly), materiály, měření, prostředí.
- Napsat jednotlivé příčiny (kategorie) jako větve z hlavní šipky.
- Provést brainstorming ohledně detailů příčin a použít otázku „Proč se to stalo?“. Zakreslit každou detailní příčinu jako odbočující šipku dané kategorie. Příčiny mohou být psány na několika místech, pokud se týkají více kategorií.
- Ke každému detailu znovu použít otázku „proč se to stalo?“ a napsat další příčiny. Otázkou „Proč?“ je možné pokračovat hlouběji.
- Když skupině dojdou nápady, je třeba se zaměřit na místa v grafu, kde je méně zaznamenaných příčin.
Kontrolní tabulka

Kontrolní tabulka nebo formulář pro sběr údajů slouží ke sběru a zaznamenání prvotních kvantitativních údajů o jakosti, např. počet a druh vad nebo problémů, které se vyskytly během výrobního procesu nebo při výstupní kontrole. Cílem je získat celkový přehled o stavu kvality a dát odpovědným osobám možnost rozhodovat se na základě faktů.[10] Při návrhu formuláře, sběru a zaznamenání dat je třeba zvážit několik hledisek:[11]
- Princip stratifikace – proces třídění dat, jehož cílem je oddělení dat různých zdrojů tak, aby bylo možno rychle identifikovat původ každé položky a tím i původ případného souvisejícího problému.
- Principy jednoduchosti, standardizace a vizuální interpretace – je kladen důraz na jednoduchost zápisu dat, aby ho mohl provést každý. Záznam má být proveden jednoduše za použití značek či čárek namísto číselných údajů. Data by měla být zapsána v takové formě, aby se již při dalším zpracování nemusela přepisovat do dalších formulářů.
Histogram

Histogram je grafické znázornění distribuce dat pomocí sloupcového grafu se sloupci stejné šířky, vyjadřující šířku intervalů (tříd), přičemž výška sloupců vyjadřuje četnost sledované veličiny v daném intervalu.[12] Je důležité zvolit správnou šířku intervalu, neboť nesprávná šířka intervalu může snížit informační hodnotu diagramu.[11]
Histogram se užívá tam, kde jsou k dispozici číselné údaje o běhu procesu, při určení, zda je distribuce přibližně normální a zda proces vyhovuje požadavkům. Také je možné sledovat, kdy došlo v procesu ke změnám, případně graficky porovnávat výstupy dvou různých procesů. Histogram je vhodný pro snadno pochopitelné zobrazení distribuce dat procesu. Při konstrukci histogramu je vhodné mít alespoň 50 za sebou jdoucích hodnot metriky procesu, přičemž je nutné zvolit vhodně šířku intervalu. Podle tvaru histogramu je možné posoudit některé vlastnosti procesu a dat, kupříkladu dva vrcholy histogramu místo jednoho signalizují, že data byla sloučena ze dvou rozdílných procesů.[7]

Paretův diagram
Paretův diagram, pojmenovaný podle Vilfreda Pareta, je typ grafu, který je kombinací sloupcového a čárového grafu, kde sloupce znázorňující četnost pro jednotlivé kategorie jsou seřazeny podle velikosti (nejvyšší sloupec vlevo, nejnižší vpravo) a linie představuje kumulativní četnost v procentech. Paretův diagram se používá ke znázornění důležitosti jednotlivých kategorií.[7]
Paretův diagram je vhodné použít při analýze četnosti incidentů daného procesu, které mohou mít vícero příčin a je třeba určit nejvýznamnější příčiny. Při konstrukci Paretova grafu je nutné určit kategorie, které se budou zobrazovat, jaké veličiny se budou měřit a jakého časového úseku se bude měření týkat.[7]
Korelační diagram

Korelační diagram nebo též bodový graf je matematické schéma užívající kartézských souřadnic pro zobrazení souboru dat o dvou proměnných. Data jsou zobrazena jako jednotlivé body, kde horizontální osu určuje hodnota první proměnné a vertikální osu hodnota druhé proměnné.[13] Takto je možné jednoduše zjistit vzájemný vztah (korelaci) mezi oběma proměnnými,[7] případně tuto závislost interpolovat (přímkou, křivkou, nebo jiným typem závislosti).
Korelační diagram je vhodné použít, když je třeba spárovat numerická data, kde případně závislá proměnná má více hodnot pro každou jednu hodnotu nezávislé proměnné. Korelační diagram může snadno odpovědět na otázku, zda tyto dvě proměnné souvisí či nikoliv. Lze tak například určit, zda jsou příčina a následek z Išikawova diagramu příbuzné, či nikoliv.[7]
Při konstrukci diagramu je vhodné dát nezávislou proměnnou na osu x a závislou na osu y a vynést hodnoty v podobě bodů. Když bod padne na stejné místo, měl by být nakreslen hned vedle, aby byly vidět oba. Body buď vytvoří opticky přímo viditelnou závislost, nebo je možné provést rozdělení oblasti na čtyři stejně velké kvadranty tak, aby případná nelineární závislost byla lépe patrná. Výsledkem může být i potvrzení, že proměnné nejsou vzájemně závislé.[7]

Vývojový diagram
Vývojový diagram je grafické znázornění algoritmu nebo procesu a slouží k lepšímu pochopení procesů a jejich vztahů. Vývojový diagram používá pro znázornění jednotlivých dílčích operací symboly, které jsou navzájem propojeny pomocí orientovaných šipek.
Tento nástroj bývá v některých seznamech zaměněn za stratifikaci, tedy rozvrstvení dat. Jedná se o implementaci bodového diagramu pro případ více než jednoho zdroje dat, aby bylo možné najít jejich rozdíly. Může se jednat o data z různých dní, různých dodavatelů nebo populačních skupin. Data je vhodně rozdělit do skupin prakticky již předtím, než se započne s jejich sběrem.[7]
Regulační diagram


Regulační diagram jako nástroj statistické regulace procesu (SPC z anglického Statistic Process Control) je graf, který se používá ke znázornění změn procesu, resp. jeho klíčové metriky v průběhu času. Regulační diagram má vždy označenu střední hodnotu (CL – Central Line) a horní a dolní regulační mez (UCL – Upper Control Line a LCL – Lower Control Line), tzv. akční meze, které jsou určeny buď z historických dat, nebo jsou cílovou hodnotou určenou předpisem. Je též možnost vyznačit tzv. výstražné meze, tedy horní výstražnou mez (UWL – Upper Warning Limit) a dolní výstražnou mez (LWL – Lower Warning Limit).[11] Z časového průběhu diagramu je možné udělat závěr, zda je chování procesu či metriky regulované, nebo zda je nepředvídatelné (mimo kontrolu).[14]
Regulační diagramy tak mohou být použity například ke kontrole stability procesu, tedy mohou zjistit, zda proces funguje jako stabilní systém s náhodnými vlivy působícími v malém rozsahu (systém s inherentní variabilitou) označovaný též jako proces ve „statisticky zvládnutém stavu“, případně zda dochází ke zlepšení či zhoršení tohoto stavu. Dále pak mohou být použity ke sledování trendů, iterací a cyklů chování systému a tak určovat predikovatelnost systému a předpovídat, zda systém vyhoví stanoveným požadavkům. Také se používají k identifikaci a případné eliminaci nepříznivých vlivů, k poskytnutí zpětné vazby pro nastavení procesu a při posuzování výkonnosti systému měření. Regulační diagram poskytuje uživatelům on-line pohled na chování procesu a jeho výhodou je jednoduchost konstrukce a snadnost užití.[15] Regulační diagram je také vhodné použít pro ovládání probíhajících procesů a opravu chyb tzv. „za běhu“.[7]
Pro regulační diagramy platí další rozhodná kritéria pro určení stability procesu, resp. nutnosti zásahu do procesu. Jsou to tzv. testy nenáhodných uskupení, tedy zvláštních uskupení bodů. Takovým uskupením může být:
- Jeden nebo více bodů leží mimo akční meze.
- Určitý počet bodů v řadě za sebou leží mimo výstražné meze.
- Určitý počet bodů v řadě za sebou leží na jedné straně od střední hodnoty.
- Určitý počet bodů v řadě za sebou leží na jedné straně od střední hodnoty a vykazuje více než jedno překročení výstražných mezí.
- Určitý počet bodů v řadě za sebou bez přerušení roste, případně klesá.
- Vyšší počet bodů v řadě za sebou nevykazuje žádná narušení mezí.
- Vyšší počet bodů v řadě za sebou střídavě klesá a roste.
- Určitý počet bodů v řadě za sebou překračuje výstražné meze.
Implementace počtu bodů se může lišit případ od případu. Příkladem mohou být tzv. Nelsonova pravidla publikovaná v roce 1984.[16]
Odkazy
Reference
- ↑ a b HORÁLEK, Vratislav. Jednoduché nástroje řízení jakosti I.. Praha: Decibel Production, 2004. Dostupné v archivu pořízeném dne 2016-03-04. ISBN 80-02-01689-0. Archivováno 4. 3. 2016 na Wayback Machine.
- ↑ MOORE, Matthew. The seven basic tools of quality [online]. Improvementandinnovation.com, 30. listopadu 2007 [cit. 2013-01-10]. Dostupné v archivu pořízeném dne 2013-02-16.
- ↑ IŠIKAWA, Kaoru. What Is Total Quality Control? The Japanese Way. 1. vyd. Englewood Cliffs, New Jersey: Prentice-Hall, 1985. Dostupné online. ISBN 9780139524332. OCLC 11467749 S. 198. Dále jen Išikawa (1985).
- ↑ IŠIKAWA, Kaoru. Introduction to Quality Control. 1. vyd. Tokyo: 3A Corp, 1990. ISBN 9784906224616. OCLC 23372992 S. 98.
- ↑ Išikawa Kaoru (1985), strana 18
- ↑ Išikawa Kaoru (1985), strana 199
- ↑ a b c d e f g h i j Nancy R. Tague. Seven Basic Quality Tools [online]. Milwaukee, Wisconsin: American Society for Quality, 2004 [cit. 2010-02-05]. (The Quality Toolbox). S. 15. Dostupné v archivu pořízeném dne 2018-10-31.
- ↑ MONTGOMERY, Douglas. Introduction to Statistical Quality Control. Hoboken, New Jersey: John Wiley & Sons, Inc., 2005. Dostupné online. ISBN 9780471656319. OCLC 56729567 S. 148.
- ↑ Diagramy příčin a následků [online]. ikvalita.cz [cit. 2010-12-19]. Dostupné v archivu pořízeném dne 2011-10-09.
- ↑ Kontrolní tabulky [online]. ikvalita.cz. Dostupné online.
- ↑ a b c NENADÁL, Jaroslav. Moderní management jakosti: principy, postupy, metody. Praha: Management Press, 2008. ISBN 978-80-7261-186-7.
- ↑ KUPKA, Karel. Statistické řízení jakosti: interaktivní analýza a interpretace dat pro řízení jakosti a ekonomiku. Pardubice: TriloByte, 1997. ISBN 80-238-1818-X.
- ↑ UTTS, Jessica M. Seeing Through Statistics. 3rd Edition. vyd. [s.l.]: Thomson Brooks/Cole, 2005. Dostupné online. ISBN 0-534-39402-7. S. 166-167. (anglicky)
- ↑ TOŠENOVSKÝ, Josef; NOSKIEVIČOVÁ, Darja. Statistické metody pro zlepšování jakosti. Ostrava: Montanex, 2000. ISBN 80-7225-040-X.
- ↑ ČSN ISO 7870-1 (010272), září 1995, EAN 8590963861357, náhled online[nedostupný zdroj]
- ↑ Lloyd S. Nelson. Technical Aids. S. 238–239. Journal of Quality Technology [online]. Říjen 1984. Roč. 16, čís. 4, s. 238–239.
Literatura
- PLÁŠKOVÁ, Alena. Jednoduché nástroje řízení jakosti II.. [s.l.]: Decibel Production Dostupné online. ISBN 80-02-01690-4.[nedostupný zdroj]
- 7 nástrojů kvality
- 7 nástrojů kvality NOVÝCH
Média použitá na této stránce
Autor:
- Cumulative_vs_normal_histogram_cz.svg: *Cumulative_vs_normal_histogram.svg: Kierano
- derivative work: DeeMusil (talk)
- Check_sheet_for_motor_assembly_cz.svg: *Check_sheet_for_motor_assembly.svg: DanielPenfield
- derivative work: DeeMusil (talk)
- Linear_regression.svg: Sewaqu
- LampFlowchart_cz.svg: *LampFlowchart.svg: svg by Booyabazooka
original png by Wapcaplet - derivative work: DeeMusil (talk)
- ControlChart_cz.svg: *ControlChart.svg: Original uploader was DanielPenfield at en.wikipedia
- derivative work: DeeMusil (talk)
- Pareto_chart_of_titanium_investment_casting_defects_cz.svg: *Pareto_chart_of_titanium_investment_casting_defects.svg: DanielPenfield
- derivative work: DeeMusil (talk)
- derivative work: DeeMusil (talk)
Example en:Pareto chart
Autor:
- Pareto_chart_of_titanium_investment_casting_defects.svg: DanielPenfield
- derivative work: DeeMusil (talk)
Example en:Pareto chart
Autor:
- Check_sheet_for_motor_assembly.svg: DanielPenfield
- derivative work: DeeMusil (talk)
Example en:check sheet produced from ASQ's Excel template
Autor:
- Ishikawa_Fishbone_Diagram.svg: FabianLange at de.wikipedia
- derivative work: DeeMusil (talk)
Išikawův fishbone diagram příčin a následků
Autor:
- LampFlowchart.svg: svg by Booyabazooka
original png by Wapcaplet - derivative work: DeeMusil (talk)
A simple flowchart for troubleshooting a broken lamp.
Autor: GMcGlinn, Licence: CC BY-SA 3.0
Poster page showing all the rules (Nelson Rules) of a Control Chart
Autor:
- Cumulative_vs_normal_histogram.svg: Kierano
- derivative work: DeeMusil (talk)
A plot showing a regular and a cumulative histogram of the same data. The data shown is 10,000 points randomly sampled from a normal distribution with mean of 0 and standard deviation of 1.
Random data points and their linear regression. Created with the following Sage (http://sagemath.org) commands:
X = RealDistribution('uniform', [-20, 60])
Y = RealDistribution('gaussian', 1.5)
f(x) = 3*x/20 + 5
xvals = [X.get_random_element() for _ in range(100)]
data = [(x, f(x) + Y.get_random_element()) for x in xvals]
m, b = var('m b')
g(x) = m*x + b
g(x) = g(x).subs(find_fit(data, g, solution_dict=True))
p = list_plot(data) + plot(g, (x, -20, 60), color='red')
p.save('linear_regression.svg')
Autor:
- ControlChart.svg: Původně soubor načetl DanielPenfield na projektu Wikipedie v jazyce angličtina
- derivative work: DeeMusil (talk)
DanielPenfield 22:16, 30 June 2007 (UTC)