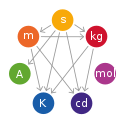
Soustava SI
Soustava SI (zkratka z francouzského „Système International“[1]:s.165, česky Mezinárodní soustava jednotek[2]) je moderní formou[1]:s.117[3][4] metrické soustavy a nejrozšířenějším systémem jednotek na světě.[1]:s.123[5][6] Byla založena a je udržována[7] Generální konferencí pro míry a váhy (CGPM[pozn. 1]) a je jedinou měrnou soustavou, která má oficiální status téměř ve všech zemích světa a používá se ve vědě, technice, průmyslu i každodenním obchodě.
| Značka | Jednotka | Fyzikální veličina |
|---|---|---|
| s | sekunda | čas |
| m | metr | délka |
| kg | kilogram | hmotnost |
| A | ampér | elektrický proud |
| K | kelvin | termodynamická teplota |
| mol | mol | látkové množství |
| cd | kandela | svítivost |
Soustava SI zahrnuje ucelenou soustavu fyzikálních jednotek, která začíná sedmi základními jednotkami: sekunda (značka s, jednotka času), metr (m, délka), kilogram (kg, hmotnost), ampér (A, elektrický proud), kelvin (K, termodynamická teplota), mol (mol, látkové množství) a kandela (cd, svítivost). Systém může obsahovat koherentní jednotky pro neomezený počet dalších veličin. Tyto jednotky se nazývají koherentní odvozené jednotky, které lze vždy reprezentovat jako součin nebo podíl základních jednotek. Dvacet dva koherentních odvozených jednotek dostalo vlastní název a značku.[pozn. 2]
Sedm základních jednotek a 22 koherentních odvozených jednotek se speciálními názvy a značkami lze použít v kombinaci k vyjádření dalších koherentních odvozených jednotek. Vzhledem k tomu, že velikosti koherentních jednotek jsou vhodné pouze pro některá použití a ne pro jiná, poskytuje soustava SI dvacet čtyři předpon, které po přidání k názvu a značky koherentní jednotky vytvářejí dvacet čtyři dalších (nekoherentních) jednotek SI pro stejnou veličinu; tyto nekoherentní jednotky jsou vždy desetinnými (tj. mocninami deseti) násobky a díly koherentní jednotky. Soustava SI je zamýšlena jako vyvíjející se systém; jednotky a předpony jsou vytvářeny a definice jednotek jsou upravovány na základě mezinárodní dohody tak, jak postupuje technologie měření a zvyšuje se přesnost měření.
| Značka | Konstanta | Přesná hodnota |
|---|---|---|
| ΔνCs | frekvence záření velmi jemného přechodu Cs | 9192631770 Hz |
| c | rychlost světla | 299792458 m/s |
| h | Planckova konstanta | 6,62607015×10−34 J⋅s |
| e | elementární náboj | 1,602176634×10−19 C |
| k | Boltzmannova konstanta | 1,380649×10−23 J/K |
| NA | Avogadrova konstanta | 6,02214076×1023 mol−1 |
| Kcd | světelná účinnost záření o frekvenci 540 THz | 683 lm/W |
Od roku 2019 jsou velikosti všech jednotek SI definovány na základě stanovení, že sedm přírodních konstant SI má určité přesné číselné hodnoty, pokud jsou vyjádřeny v jednotkách SI. Těmito přírodními konstantami jsou rychlost světla ve vakuu c, frekvence záření velmi jemného přechodu cesia ΔνCs, Planckova konstanta h, elementární náboj e, Boltzmannova konstanta k, Avogadrova konstanta NA a světelná účinnost Kcd. Povaha přírodních konstant sahá od základních přírodních konstant, jako je c, až po čistě technickou konstantu Kcd. Před rokem 2019 nebyly h, e, k a NA definovány a priori, ale jednalo se spíše o velmi přesně měřené veličiny. V roce 2019 byly jejich hodnoty definičně stanoveny na jejich nejlepší odhady v daném okamžiku, čímž byla zajištěna kontinuita s předchozími definicemi základních jednotek.
Současný způsob definování SI je výsledkem desetiletí trvajícího posunu ke stále abstraktnějším a idealizovanějším formulacím, v nichž jsou realizace jednotek pojmově odděleny od definic. Důsledkem je, že s rozvojem vědy a technologií mohou být zaváděny nové a lepší realizace, aniž by bylo nutné jednotky nově definovat. Jedním z problémů etalonů je, že se mohou ztratit, poškodit nebo změnit; dalším je, že vnášejí nejistotu, kterou nelze snížit pokrokem ve vědě a technologii. Posledním etalonem používaným v soustavě SI byl mezinárodní prototyp kilogramu, válec z platiny a iridia.
Původní motivací pro vývoj soustavy SI byla rozdílnost jednotek, které vznikly v rámci soustavy centimetr-gram-sekunda (CGS) (konkrétně nesoulad mezi soustavami elektrostatických jednotek a elektromagnetických jednotek), a nedostatečná koordinace mezi různými obory, které je používaly. Generální konference pro míry a váhy, která byla založena Úmluvou o metru z roku 1875, sdružila mnoho mezinárodních organizací s cílem stanovit definice a standardy nového systému a sjednotit pravidla pro zápis a prezentaci měr. Tento systém byl zveřejněn v roce 1960 jako výsledek iniciativy, která vznikla v roce 1948, a je tedy založen na soustavě jednotek metr-kilogram-sekunda (MKS), nikoli na některé z variant CGS.
Principy

Mezinárodní soustava jednotek neboli soustava SI[1]:s.123 je desítková[pozn. 3] a metrická[pozn. 4] soustava jednotek zavedená v roce 1960 a od té doby pravidelně aktualizovaná. Soustava SI má oficiální status ve většině zemí světa, včetně Spojených států, Kanady a Spojeného království, ačkoli tyto tři země patří mezi hrstku států, které v různé míře nadále používají i své zvykové soustavy. Nicméně díky této téměř univerzální úrovni přijetí se soustava SI „používá na celém světě jako preferovaná soustava jednotek, základní jazyk vědy, techniky, průmyslu a obchodu“.[1]:s.123
Jedinými dalšími typy měrných soustav, které jsou stále široce rozšířené po celém světě, jsou imperiální a americká běžná měrná soustava[pozn. 5] a i ty jsou z právního hlediska definovány pomocí soustavy SI.[pozn. 6] Existují i další, méně rozšířené měrné soustavy, které se příležitostně používají v určitých oblastech světa. Kromě toho existuje mnoho jednotlivých jednotek, které nepatří do žádné ucelené soustavy jednotek, ale přesto se v určitých oborech a regionech stále pravidelně používají. Obě tyto kategorie jednotek jsou také obvykle právně definovány v termínech jednotek SI.
Řídicí orgán
Soustavu SI zřídila a spravuje Generální konference pro míry a váhy (CGPM).[7] V praxi se CGPM řídí doporučeními Poradního výboru pro jednotky (CCU), který je skutečným orgánem, jenž vede technická jednání o novém vědeckém a technologickém vývoji souvisejícím s definicí jednotek a SI. CCU podává zprávy Mezinárodnímu výboru pro míry a váhy (CIPM), který zase podává zprávy CGPM.
Soustava SI je regulována a průběžně rozvíjena třemi mezinárodními organizacemi, které byly založeny v roce 1875 na základě Dohody o metru. Jsou to Generální konference pro míry a váhy (CGPM), Mezinárodní výbor pro míry a váhy (CIPM) a Mezinárodní úřad pro míry a váhy (BIPM). Konečnou pravomoc má CGPM, což je plenární orgán, jehož prostřednictvím členské státy společně jednají v záležitostech týkajících se vědy o měření a měřících standardech; obvykle se schází každé čtyři roky.[9] CGPM volí CIPM, což je osmnáctičlenný výbor složený z významných vědců. CIPM funguje na základě rad řady svých poradních výborů, které sdružují světové odborníky v daných oborech jako poradce pro vědecké a technické záležitosti.[10] Jedním z těchto výborů je Poradní výbor pro jednotky (CCU), který je zodpovědný za záležitosti související s vývojem Mezinárodní soustavy jednotek (SI), přípravu dalších vydání příručky soustavy SI a poradenství CIPM v záležitostech týkajících se jednotek měření.[11] Právě CCU se podrobně zabývá veškerým novým vědeckým a technologickým vývojem souvisejícím s definicí jednotek a soustavou SI. V praxi, pokud jde o definici SI, CGPM pouze formálně schvaluje doporučení CIPM, který se zase řídí radami CCU.
Členy CCU jsou:[12][13] národní laboratoře členských států CGPM pověřené stanovením národních norem;[pozn. 7] příslušné mezivládní organizace a mezinárodní orgány; mezinárodní komise nebo výbory; vědecké svazy; osobní členové; a jako člen ex offo všech poradních výborů ředitel BIPM.
Všechna rozhodnutí a doporučení týkající se jednotek jsou shromážděna v příručce nazvané Mezinárodní soustava jednotek (SI),[1] kterou BIPM vydává ve francouzštině a angličtině a pravidelně ji aktualizuje. Psaní a údržbu této příručky zajišťuje jeden z výborů CIPM. Definice pojmů "veličina", "jednotka", "rozměr" atd., které jsou v této příručce SI použity, odpovídají definicím uvedeným v Mezinárodním slovníku základních a všeobecných termínů v metrologii.[14] Příručka ponechává určitý prostor pro místní odchylky, zejména pokud jde o názvy jednotek a termíny v různých jazycích.[15]
Jednotky a předpony

Mezinárodní soustava jednotek se skládá ze souboru základních jednotek SI, odvozených jednotek SI a souboru násobků a dílů založených na desetinném čísle, které se používají jako předpony SI.[16]:s.103–106 Jednotky, s výjimkou předponových jednotek,[pozn. 8] tvoří soustavu jednotek koherentních, která je založena na soustavě veličin tak, že rovnice mezi číselnými hodnotami vyjádřenými v koherentních jednotkách mají přesně stejný tvar, včetně číselných koeficientů, jako odpovídající rovnice mezi veličinami. Například 1 N = 1 kg × 1 m/s2 říká, že jeden newton je síla potřebná ke zrychlení hmotnosti jednoho kilogramu na jeden metr za sekundu na druhou, jak je to vztaženo prostřednictvím principu koherence k rovnici vztahující se k odpovídajícím veličinám: F = m × a.
Odvozené jednotky se vztahují na odvozené veličiny, které mohou být z definice vyjádřeny pomocí základních veličin, a nejsou tedy nezávislé; například elektrická vodivost je inverzní hodnotou elektrického odporu, z čehož vyplývá, že siemens je inverzní hodnotou ohmu, a podobně lze ohm a siemens nahradit poměrem ampéru a voltu, protože tyto veličiny jsou ve vzájemném definovaném vztahu. Další užitečné odvozené veličiny lze specifikovat v termínech základních a odvozených jednotek SI, které nemají v SI pojmenované jednotky, například zrychlení, které je v jednotkách SI definováno jako m/s2.
Základní jednotky
Soustava SI používá sedm základních jednotek, které odpovídají sedmi základním fyzikálním veličinám: sekunda (značka s, jednotka SI pro fyzikální veličinu čas), metr (značka m, jednotka SI pro délku), kilogram (kg, jednotka hmotnosti), ampér (A, elektrický proud), kelvin (K, termodynamická teplota), mol (mol, látkové množství) a kandela (cd, svítivost).[1] Všechny jednotky v soustavě SI lze vyjádřit pomocí základních jednotek a základní jednotky slouží jako preferovaná sada pro vyjádření nebo analýzu vztahů mezi jednotkami.
Níže následuje definice[17][18] a popis základních jednotek pro sedm základních veličin a jejich stručný historický vývoj.
| Jednotka | Značka (závazná) | Značka rozměru | Fyzikální veličina | Typická značka | Stručná definice |
|---|---|---|---|---|---|
| sekunda[p 1] | s | T | čas | Doba trvání 9 192 631 770 period záření odpovídající přechodu mezi dvěma hladinami velmi jemné struktury základního stavu atomu cesia 133 | |
| metr | m | L | délka | , , , , , , , atd.[p 2] | Vzdálenost, kterou urazí světlo ve vakuu za 1 / 299 792 458 sekundy. |
| kilogram[p 3] | kg | M | hmotnost | Kilogram je definován stanovením Planckovy konstanty h přesně na 6,62607015×10−34 J⋅s (J = kg⋅m2⋅s−2), vzhledem k definicím metru a sekundy.[19] | |
| ampér | A | I | elektrický proud | Proud přesně 1/ (1,602176634×10−19) násobku elementárního náboje e za sekundu. Což se rovná přibližně 6,2415090744×1018 elementárních nábojů za sekundu. | |
| kelvin | K | Θ | termodynamická teplota | Kelvin je definován stanovením pevné číselné hodnoty Boltzmannovy konstanty k na 1,380649×10−23 J⋅K−1, (J = kg⋅m2⋅s−2), vzhledem k definici kilogramu, metru a sekundy. | |
| mol | mol | N | látkové množství | Množství látky přesně 6,02214076×1023 elementárních entit.[p 4] Toto číslo je pevná číselná hodnota Avogadrovy konstanty NA vyjádřená v jednotce mol−1. | |
| kandela | cd | J | svítivost | Svítivost zdroje, který vydává monochromatické záření o frekvenci 5,4×1014 hertzů, jehož intenzita daném směru je 1/683 wattů na steradián. | |
| |||||
Sekunda
Sekunda, značka „s“, je jednotka času v SI. Je definována stanovením pevné číselné hodnoty frekvence ΔνCs, přechodu mezi dvěma hladinami velmi jemné struktury základního stavu atomu cesia 133 nacházejícího se v klidovém stavu, která je rovna 9 192 631 770, je-li vyjádřena v jednotce Hz, která je rovna s−1.[pozn. 9]
Nejstarší definice sekundy ji odvozovaly z délky středního slunečního dne, jako jeho 1/86 400. V 50. letech 20. století se za stabilnější základ definice začal považovat místo dne rok, což byl koncept v roce 1960 převzatý do definice sekundy v SI:
- Sekunda je zlomek 1/31 556 925,9747 tropického roku pro 0. leden 1900 ve 12 hodin efemeridového času.[20]
Brzy však technologický pokrok umožnil přesnější měření a udržování času pomocí atomových hodin. V roce 1967 tak byla definice změněna na:
- Sekunda je doba trvání 9 192 631 770 period záření odpovídajícího přechodu mezi dvěma hladinami velmi jemné struktury základního stavu atomu cesia 133.
Později bylo upřesněno, že atom cesia musí být v klidu (časem se rozumí vlastní čas z pohledu obecné teorie relativity) a teplota pozadí blízká 0 K. Ze třetího zákona termodynamiky plyne, že teplota absolutní nuly je nedosažitelná. Lze se k ní však libovolně přiblížit. Podmínku nulové termodynamické teploty je třeba chápat tak, že cesiové hodiny musí provádět korekce s ohledem na teplotu pozadí.
Stávající znění definice sekundy získala při redefinici jednotek SI v roce 2019; fakticky zůstala nezměněna, liší se jen formálně, aby měla stejný formát jako ostatní nové definice, čímž vynikne idea, že každá jednotka je svázána s určitou neměnnou vlastností přírody. Vzhledem k pokroku v metrologii času a frekvence se však uvažuje o budoucí faktické redefinici i u sekundy, která by měla vstoupit v platnost ještě před rokem 2030, podle předběžných předpokladů nejspíše v roce 2026.[21][22]
Metr
Metr, značka „m“, je jednotka délky v SI. Je definován stanovením pevné číselné hodnoty rychlosti světla ve vakuu c, která je rovna 299 792 458, je-li vyjádřena v jednotce m s−1, kde sekunda je definována prostřednictvím ΔνCs.

Jako standardní vědecká jednotka se původně koncipovala délka kyvadla o půlperiodě jedné sekundy. Jelikož se však brzy zjistilo, že doba kyvu poměrně značně závisí na místě měření, byla jako definice metru zvolena délka definovaná jako desetimiliontina délky kvadrantu zemského poledníku procházejícího Paříží (to odpovídá obvodu Země přesně 40 000 km). Na základě geodetických měření byl pak vyroben prototyp metru, platino-iridiová tyč o průřezu písmene X, na níž rysky definovaly délku jednoho metru, pokud se měřil za teploty tání ledu.
Definice prototypem však postupně přestala vyhovovat potřebám a vzrůstající přesnosti metrologie, takže v roce 1960 byla přijata nová definice založená na přírodním jevu:
- Metr je vzdálenost rovná 1 650 736,73 vlnovým délkám ve vakuu záření odpovídajícího přechodu mezi energetickými hladinami 2p10 a 5d5 atomu kryptonu 86.[23]
V roce 1983 pak byla tato definice opět nahrazena, tentokrát za definici založenou na rychlosti světla:
- Metr je vzdálenost, kterou urazí světlo ve vakuu za dobu 1/299 792 458 sekundy.
Také zde došlo v roce 2019 k reformulaci, ale beze změny definice. Definicí metru je tedy přesně stanovena vlnová délka mikrovlnného záření, které je uvedeno v definici sekundy, vztahem
- .
Porovnání neznámé vzdálenosti s touto vlnovou délkou lze provádět interferometricky.
Kilogram

Kilogram, značka „kg“, je jednotka hmotnosti v SI. Je definován stanovením pevné číselné hodnoty Planckovy konstanty h, která je rovna 6,626 070 15×10−34, je-li vyjádřena v jednotce J s, která je rovna kg m2 s−1, kde metr a sekunda jsou definovány prostřednictvím c a ΔνCs.
Standardní jednotka hmotnosti (původně nazývaná grave) byla koncipována jako hmotnost jednoho litru vody prosté vzduchu za teploty tuhnutí. Jako definici této jednotky však první Generální konference pro míry stanovila hmotnost prototypu kilogramu, válečku z platino-iridiové slitiny:
- Kilogram je jednotka hmotnosti; je rovna hmotnosti mezinárodního prototypu kilogramu.
Tato definice prototypem vydržela až do redefinice v roce 2019, přestože z praktických i teoretických aspektů byla již dlouho značně problematická; trvalo však dlouho, než se našla dostatečně přesná alternativa. Nová definice tak je nejpodstatnější z přijatých změn. Spojení se základní fyzikální konstantou nově umožnilo, aby velikost kilogramu a všech jednotek od něj odvozených byla spolehlivě časově stabilní. Planckova konstanta h je základní konstantou kvantové teorie, kde určuje mimo jiné vztah mezi energií a frekvencí fotonu: E=hf. Speciální teorie relativity poskytuje vztah mezi energií a hmotností, kde konstantou úměrnosti je rychlost světla ve vakuu: E=mc². Tyto dva fyzikální zákony umožňují odvodit definici kilogramu od číselné hodnoty Planckovy konstanty. Měření hmotnosti podle nových definic prakticky umožňují wattové váhy, přičemž se využívá i nová definice ampéru.
Ampér
Ampér, značka „A“, je jednotka elektrického proudu v SI. Je definován stanovením pevné číselné hodnoty elementárního náboje e, která je rovna 1,602 176 634×10−19, je-li vyjádřena v jednotce C, která je rovna A s, kde sekunda je definována prostřednictvím ΔνCs.
Ampér byl původně převzat z jednotky proudu v soustavě CGS, kde byla jednotka definována jako takový proud, tekoucí vodičem o délce 1 cm ve tvaru části kruhového oblouku o poloměru 1 cm, který ve středu kružnice vytváří magnetické pole o intenzitě 1 oersted; ampér byl však jako desetkrát menší než jednotka v systému CGS (dnes nazývaná abampér).
V roce 1946 byla definice nahrazena novou, která velikost ampéru odvozuje od elektrické síly mezi rovnoběžnými vodiči:
- Ampér je stálý elektrický proud, který protéká dvěma rovnoběžnými nekonečně dlouhými vodiči o zanedbatelném průřezu umístěnými ve vakuu 1 m od sebe, jestliže mezi vodiči působí magnetická síla o velikosti 2×10−7 newtonu na jeden metr délky vodiče.
Jinak řečeno tato definice zafixovala velikost permeability vakua na hodnotě přesně H/m.
Z praktického pohledu však definice byla problematická a etalony proudu se konstruovaly spíše na základě Josephsonova a kvantového Hallova jevu, pomocí kterých se vytvářely etalony elektrického napětí a elektrického odporu a realizace ampéru pak spočívala na aplikaci Ohmova zákona . Nová definice tak namísto permeability vakua fixuje hodnotu elementárního náboje (permeabilita vakua se tak s novou definicí stala z fixní hodnoty empiricky měřenou veličinou), čímž se stanovuje přesně také hodnota Josephsonovy konstanty a von Klitzingovy konstanty . Druhou možností realizace ampéru je využití jednoelektronové pumpy s přesným taktováním, čímž by byl uzavřen tzv. metrologický trojúhelník.[pozn. 10]
Kelvin
Kelvin, značka „K“, je jednotka termodynamické teploty v SI. Je definován stanovením pevné číselné hodnoty Boltzmannovy konstanty k, která je rovna 1,380 649×10−23, je-li vyjádřena v jednotce J K−1, která je rovna kg m2s−2 K−1, kde kilogram, metr a sekunda jsou definovány prostřednictvím h, c a ΔνCs.
Původní jednotkou teploty v metrickém systému byl stupeň Celsia, definovaný přiřazením hodnoty 0 °C teplotě tání ledu a 100 °C teplotě varu vody. V roce 1954 vznikla moderní definice kelvinu (tehdy označovaného ještě jako „stupeň Kelvina“, °K) tím, že se teplotě trojného bodu vody přiřadila teplota 273,16 °K. V roce 1967 pak jednotka získala dnešní název kelvin[27] a byla definována jako:
- Kelvin, jednotka termodynamické teploty, je rovna zlomku 1/273,16 termodynamické teploty trojného bodu vody.[28]
Z praktického pohledu však tato definice přinášela problémy, zejména se získáváním vzorku čisté vody daného izotopového složení.
Nová definice kelvinu umožňuje převést měření teploty na měření energie částic, což je v mnoha případech jednodušší, zejména při teplotách extrémně vysokých nebo nízkých. Boltzmannova konstanta je základní konstantou statistické fyziky, kde spojuje entropii s rozdělením pravděpodobnosti mikrostavů systému. Jako konstanta úměrnosti se objevuje ve stavové rovnici ideálního plynu. Určuje také vztah mezi teplotou plynu a pohybovou energií jeho molekul (ekvipartiční teorém).
Mol
Mol, značka „mol“, je jednotka látkového množství v SI. Jeden mol obsahuje přesně 6,022 140 76×1023 elementárních entit; toto číslo je pevná číselná hodnota Avogadrovy konstanty NA, je-li vyjádřena v jednotce mol−1, a nazývá se Avogadrovo číslo; látkové množství (n) systému je mírou počtu specifikovaných elementárních entit; elementární entitou může být atom, molekula, ion, elektron, jakákoli jiná částice nebo specifikované seskupení částic.
Látková množství se z praktických důvodů zjišťovala na základě hmotnosti a vyjadřovala v jednotkách „gramatom“ (mol atomů) či „grammolekula“ (mol molekul). Původně se relativní atomové hmotnosti počítaly vůči kyslíku, kterému byla konvencí stanovena relativní atomová hmotnost 16, ale nebylo jednoznačné, zda se jedná o čistý izotop kyslík-16, nebo směs izotopů v běžném vzdušném kyslíku. Od roku 1960 se proto začala používat definice založená na uhlíku, kdy byla čistému izotopu uhlík-12 stanovena relativní atomová hmotnost přesně 12. V roce 1971 tak byla definována nová základní jednotka SI, mol, definovaná jako
- Mol je látkové množství systému, který obsahuje stejný počet elementárních entit, kolik je atomů v 0,012 kg uhlíku 12C.[29]
Tato definice svazovala látkové množství s hmotností. Postupně však technický pokrok umožnil jednodušší a univerzálnější definici molu, přímým definováním počtu částic v jednotkovém látkovém množství (), tedy zafixováním Avogadrovy konstanty: 1 mol je jednoduše takové látkové množství, které obsahuje právě přesně 6,022 140 76×1023 elementárních entit.
Podle nové definice tak není látkové množství závislé na hmotnosti (ani jiných základních veličinách).
Kandela
Kandela, značka „cd“, je jednotka svítivosti v SI. Je definována stanovením pevné číselné hodnoty světelné účinnosti monochromatického záření o frekvenci 540×1012 Hz (Kcd), která je rovna 683, je-li vyjádřena v jednotce lm W−1, která je rovna cd sr W−1 nebo cd sr kg−1 m−2 s3, kde kilogram, metr a sekunda jsou definovány prostřednictvím h, c a ΔνCs.
Jako standardy svítivosti se používaly různé „standardní svíčky“ o definovaném složení a parametrech, později také definovaná žárovková vlákna. Jako univerzálnější jednotka byla navržena svítivost 1 cm² platiny ohřáté na bod tání. Kvůli přiblížení hodnoty nové jednotky k původním standardním svíčkám byla definice „nové svíčky“ doplněna o koeficient 1/60 a v roce 1948 definována pod novým mezinárodním názvem kandela. V roce 1954 byla zařazena mezi základní jednotky,[30] v roce 1967 pak byla definice zpřesněna:
- Kandela je svítivost, v kolmém směru, povrchu 1/600 000 metru čtverečního černého tělesa o teplotě tuhnoucí platiny za tlaku 101 325 newtonů na metr čtvereční.[31]
Problémy s realizací přesného černého zářiče o takto vysoké teplotě ale vedly k nové radiometrické definici jednotky, která byla přijata v roce 1979:
- Kandela je svítivost zdroje, který vydává monochromatické záření o frekvenci 540×1012 Hz, jehož intenzita v daném směru je 1/683 wattů na steradián.[32]
Změna při redefinici v roce 2019 opět znamenala pouze úpravu formulace do standardního tvaru, beze změny významu.
Odvozené jednotky
Soustava SI umožňuje neomezený počet dalších jednotek, tzv. odvozených jednotek, které lze vždy reprezentovat jako součin nebo podíl základních jednotek, případně s netriviálním číselným násobkem. Pokud je tento násobitel roven jedné, jednotka se nazývá koherentní odvozená jednotka.[pozn. 11] Základní a koherentní odvozené jednotky SI tvoří dohromady koherentní soustavu jednotek (soubor koherentních jednotek SI).[as] Dvaadvacet koherentních odvozených jednotek v průběhu historie dostalo samostatné názvy, které zjednodušují jejich používání v praktickém životě.[17]:s.26–27, 137–138 Sedm základních jednotek a 22 odvozených jednotek se speciálními názvy a značky lze použít v kombinaci k vyjádření dalších odvozených jednotek,[pozn. 2] které byly přijaty pro usnadnění měření různých veličin.
Před novou definicí v roce 2019 byla soustava SI definována prostřednictvím sedmi základních jednotek, z nichž byly odvozené jednotky konstruovány jako součin mocnin základních jednotek. Po redefinici je SI definována stanovením číselných hodnot sedmi definičních konstant. To má za následek, že rozlišování mezi základními a odvozenými jednotkami není v zásadě nutné, protože všechny jednotky, základní i odvozené, lze konstruovat přímo z definičních konstant. Nicméně toto rozlišení je zachováno, protože "je užitečné a historicky dobře zavedené", a také proto, že řada norem ISO/IEC 80000 specifikuje základní a odvozené veličiny, které mají nutně odpovídající jednotky.[1]:s.129
Odvozené jednotky v soustavě SI jsou tvořeny mocninami, součinem nebo kvocientem základních jednotek a jejich počet je potenciálně neomezený.[16]:s.103[15]:s.14,16 Odvozené jednotky jsou spojeny s odvozenými veličinami; například rychlost je veličina, která je odvozena ze základních veličin času a délky, a proto je odvozenou jednotkou soustavy SI metr za sekundu (značka m/s). Rozměry odvozených jednotek lze vyjádřit pomocí rozměrů základních jednotek.
K vyjádření dalších odvozených jednotek lze použít kombinace základních a odvozených jednotek. Například jednotkou síly v soustavě SI je newton (N), jednotkou tlaku v soustavě SI je pascal (Pa) - a pascal lze definovat jako jeden newton na metr čtvereční (N/m2).[33]
| Název | Značka | Veličina | Vyjádření v jiných jednotkách | Vyjádření v základních jednotkách SI |
|---|---|---|---|---|
| radián | rad | rovinný úhel | m·m−1 | bezrozměrný |
| steradián | sr | prostorový úhel | m2·m−2 | bezrozměrný |
| hertz | Hz | frekvence | 1/s | s−1 |
| newton | N | síla, váha | kg·m/s2 | kg·m·s−2 |
| pascal | Pa | tlak, napětí | N/m2 | m−1·kg·s−2 |
| joule | J | energie, práce, teplo | N·m = C·V = W·s | m2·kg·s−2 |
| watt | W | výkon, zářivý tok | J/s = V·A | m2·kg·s−3 |
| coulomb | C | elektrický náboj | s·A | s·A |
| volt | V | elektrické napětí, elektrický potenciál | W/A = J/C | m2·kg·s−3·A−1 |
| farad | F | elektrická kapacita | C/V | m−2·kg−1·s4·A2 |
| ohm | Ω | elektrický odpor, impedance, reaktance | V/A | m2·kg·s−3·A−2 |
| siemens | S | elektrická vodivost | 1/Ω | m−2·kg−1·s3·A2 |
| weber | Wb | magnetický tok | J/A | m2·kg·s−2·A−1 |
| tesla | T | magnetická indukce | V·s/m2 = Wb/m2 = N/(A·m) | kg·s−2·A−1 |
| henry | H | indukčnost | V·s/A = Wb/A | m2·kg·s−2·A−2 |
| stupeň Celsia | °C | Celsiova teplota | K (t/°C = T/K − 273,15) | K |
| lumen | lm | světelný tok | lx·m2 | cd·sr |
| lux | lx | intenzita osvětlení | lm/m2 | m−2·cd·sr |
| becquerel | Bq | radioaktivita (počet rozpadů částic za sekundu) | 1/s | s−1 |
| gray | Gy | absorbovaná dávka (ionizujícího záření) | J/kg | m2·s−2 |
| sievert | Sv | dávkový ekvivalent (ionizujícího záření) | J/kg | m2·s−2 |
| katal | kat | katalytická aktivita | mol/s | s−1·mol |
Při použití předpon v koherentních jednotkách SI již výsledné jednotky nejsou koherentní, protože předpona zavádí jiný číselný faktor než jedna.[1]:s.137 Jedinou výjimkou je kilogram, jediná koherentní jednotka SI, jejíž název a značka z historických důvodů předponu obsahuje.[pozn. 12]
Úplný soubor jednotek SI se skládá jak z koherentního souboru, tak z násobků a dílů koherentních jednotek vytvořených pomocí předpon.[1]:s.138 Například metr, kilometr, centimetr, nanometr atd. jsou všechny jednotky délky SI, ačkoli pouze metr je koherentní jednotkou SI. Podobné tvrzení platí i pro odvozené jednotky: například kg/m3, g/dm3, g/cm3, Pg/km3 atd. jsou všechny jednotky SI pro hustotu, ale pouze kg/m3 je koherentní jednotkou SI.
Metr je navíc jedinou koherentní jednotkou délky v soustavě SI. Každá fyzikální veličina má přesně jednu hlavní jednotku SI, i když tato jednotka může být vyjádřitelná v různých formách pomocí některých speciálních názvů a značek.[1]:s.140 Například koherentní jednotku SI pro hybnost lze zapsat buď jako kg⋅m/s, nebo jako N⋅s, a obě formy se používají (např. srovnej zde[34]:205 a zde[35]:135).
Na druhou stranu může několik různých veličin sdílet stejnou koherentní jednotku SI. Například joule na kelvin (značka J/K) je koherentní jednotkou SI pro dvě různé veličiny: tepelnou kapacitu a entropii; dalším příkladem je ampér, který je koherentní jednotkou SI pro elektrický proud i magnetické napětí. Proto je důležité nepoužívat k určení veličiny pouze jednotku.[pozn. 13]
Kromě toho může být tatáž koherentní jednotka SI v jednom kontextu základní jednotkou, ale v jiném kontextu koherentní odvozenou jednotkou. Například ampér je základní jednotkou, když je jednotkou elektrického proudu, ale koherentní odvozenou jednotkou, když je jednotkou magnetického napětí.[1]:s.140 Jako možná známější příklad lze uvést dešťové srážky definované jako objem deště (měřený v m3), který spadl na jednotku plochy (měřenou v m2). Protože m3/m2 = m, vyplývá z toho, že koherentní odvozenou jednotkou SI pro srážky je metr, přestože metr je také základní jednotkou SI pro délku.[pozn. 14]
| Název | Značka | Veličina | Vyjádření v základních jednotkách SI |
|---|---|---|---|
| metr čtvereční | m2 | obsah | m2 |
| metr krychlový | m3 | objem | m3 |
| metr za sekundu | m/s | rychlost | m·s−1 |
| metr krychlový za sekundu | m3/s | objemový průtok | m3·s−1 |
| metr za sekundu na druhou | m/s2 | zrychlení | m·s−2 |
| metr za sekundu na třetí | m/s3 | ryv | m·s−3 |
| radián za sekundu | rad/s | úhlová rychlost | s−1 |
| newton sekunda | N·s | hybnost, impuls síly | m·kg·s−1 |
| newton metr sekunda | N·m·s | moment hybnosti | m2·kg·s−1 |
| newton metr | N·m | moment síly | m2·kg·s−2 |
| reciproční metr | m−1 | vlnové číslo | m−1 |
| kilogram na metr čtvereční | kg/m2 | plošná hustota (též plošná hmotnost) | m−2·kg |
| kilogram na metr krychlový | kg/m3 | hustota | m−3·kg |
| metr krychlový na kilogram | m3/kg | měrný objem | m3·kg−1 |
| mol na metr krychlový | mol/m3 | molární koncentrace | m−3·mol |
| metr krychlový na mol | m3/mol | molární objem | m3·mol−1 |
| joule sekunda | J·s | akce | m2·kg·s−1 |
| joule na kelvin | J/K | tepelná kapacita, entropie | m2·kg·s−2·K−1 |
| joule na kelvin mol | J/(K·mol) | molární tepelná kapacita, molární entropie | m2·kg·s−2·K−1·mol−1 |
| joule na kilogram kelvin | J/(K·kg) | měrná tepelná kapacita, specifická entropie | m2·s−2·K−1 |
| joule na mol | J/mol | molární energie | m2·kg·s−2·mol−1 |
| joule na kilogram | J/kg | specifická energie | m2·s−2 |
| joule na metr krychlový | J/m3 | hustota energie | m−1·kg·s−2 |
| newton na metr | N/m = J/m2 | povrchové napětí | kg·s−2 |
| watt na metr čtvereční | W/m2 | hustota proudění tepla, intenzita ozáření | kg·s−3 |
| watt na metr kelvin | W/(m·K) | tepelná vodivost | m·kg·s−3·K−1 |
| metr čtvereční za sekundu | m2/s | kinematická viskozita, difúzní koeficient | m2·s−1 |
| pascal sekunda | Pa·s = N·s/m2 | dynamická viskozita | m−1·kg·s−1 |
| coulomb na metr čtvereční | C/m2 | elektrická indukce | m−2·s·A |
| coulomb na metr krychlový | C/m3 | hustota elektrického náboje | m−3·s·A |
| ampér na metr čtvereční | A/m2 | hustota elektrického proudu | A·m−2 |
| siemens na metr | S/m | konduktivita | m−3·kg−1·s3·A2 |
| siemens metr čtvereční na mol | S·m2/mol | molární konduktivita | kg−1·s3·mol−1·A2 |
| farad na metr | F/m | permitivita | m−3·kg−1·s4·A2 |
| henry na metr | H/m | permeabilita | m·kg·s−2·A−2 |
| volt na metr | V/m | intenzita elektrického pole | m·kg·s−3·A−1 |
| ampér na metr | A/m | intenzita magnetického pole | A·m−1 |
| kandela na metr čtvereční | cd/m2 | jas | cd·m−2 |
| coulomb na kilogram | C/kg | ozáření, expozice (ionizujícím zářením) | kg−1·s·A |
| gray na sekundu | Gy/s | dávkový příkon | m2·s−3 |
| ohm metr | Ω·m | rezistivita | m3·kg·s−3·A−2 |
Bezrozměrné jednotky
Jednotkou bezrozměrné veličiny je zpravidla pouhá jednička (značka 1), ale uvádí se jen zřídka.[1]:s.136 Některé bezrozměrné veličiny mají specifické bezrozměrové jednotky a k nim specifické značky; např. radián a steradián jsou také jednotky bezrozměrných veličin, ale používají značky rad, resp. sr.[1]:s.137
Předpony
Stejně jako všechny metrické soustavy používá soustava SI metrické předpony k systematickému vytváření souboru jednotek, které jsou pro stejnou fyzikální veličinu desetinnými násobky a díly v širokém rozsahu.
Například zatímco koherentní jednotkou délky je metr,[pozn. 15] soustava SI poskytuje celou škálu menších a větších jednotek délky, z nichž každá může být pro dané použití výhodnější - například vzdálenost při jízdě autem se obvykle udává v kilometrech (značka km), nikoli v metrech. Metrická předpona "kilo" (značka "k") zde označuje násobek 1000; tedy 1 km = 1000 m.
Současná verze soustavy SI poskytuje dvacet čtyři metrických předpon, které označují desetinné mocniny v rozmezí od 10−30 do 1030; nejnovější předpony byly přijaty v roce 2022.[1]:s.143–144[36][37][38] Většina předpon odpovídá celým mocninám 1000; jediné, které tomu neodpovídají, jsou předpony pro 10, 1/10, 100 a 1/100.
Obecně lze říci, že pokud je dána jakákoli koherentní jednotka se samostatným názvem a značkou,[pozn. 16] lze vytvořit novou jednotku prostým přidáním příslušné metrické předpony k názvu koherentní jednotky (a odpovídající značky předpony ke značce koherentní jednotky).[pozn. 12] Jelikož metrická předpona označuje konkrétní mocninu deseti, je nová jednotka vždy násobkem nebo podílem koherentní jednotky. Převod mezi různými jednotkami SI pro jednu a tutéž fyzikální veličinu tedy vždy probíhá prostřednictvím mocniny deseti.[pozn. 17] Proto se soustavě SI (a metrické soustavě obecněji) říká desítková soustava měrných jednotek.[39]
Seskupení tvořené předponovovou značkou připojenou ke značce jednotky (např. "km", "cm") představuje novou neoddělitelnou značku jednotky. Tato nová značka může být zvýšen kladnou nebo zápornou mocninou. Může být také kombinována s jinými značkami jednotek a vytvářet složené značky jednotek.[1]:s.143 Například g/cm3 je jednotka SI pro hustotu, kde cm3 je třeba interpretovat jako (cm)3.
K názvům jednotek se přidávají předpony, které vytvářejí násobky a díly původní jednotky. Všechny tyto násobky jsou celočíselné mocniny deseti a nad sto nebo pod setinu jsou všechny celočíselné mocniny tisíce. Například kilo označuje násobek tisíce a mili označuje násobek tisícin, takže do metru je tisíc milimetrů a do kilometru tisíc metrů. Předpony se nikdy nekombinují, takže například miliontina metru je mikrometr, nikoli milimilimetr. Násobky kilogramu jsou pojmenovány tak, jako by základní jednotkou byl gram, takže miliontina kilogramu je miligram, nikoliv mikrokilogram.[16]:s.122[40]:s.14 Když se předpony používají k vytvoření násobků a dílů základních a odvozených jednotek SI, výsledné jednotky již nejsou koherentní.[16]:s.7
Mezinárodní úřad pro míry a váhy specifikuje 24 předpon pro jednotky soustavy SI:[41][42]
| Předpona | 10n | Násobek | Přijetí | |
|---|---|---|---|---|
| Jméno | Značka | |||
| quetta | Q | 1030 | 1 000 000 000 000 000 000 000 000 000 000 | 2022[43] |
| ronna | R | 1027 | 1 000 000 000 000 000 000 000 000 000 | |
| yotta | Y | 1024 | 1 000 000 000 000 000 000 000 000 | 1991 |
| zetta | Z | 1021 | 1 000 000 000 000 000 000 000 | |
| exa | E | 1018 | 1 000 000 000 000 000 000 | 1975[44] |
| peta | P | 1015 | 1 000 000 000 000 000 | |
| tera | T | 1012 | 1 000 000 000 000 | 1960 |
| giga | G | 109 | 1 000 000 000 | |
| mega | M | 106 | 1 000 000 | 1873 |
| kilo | k | 103 | 1 000 | 1795 |
| hekto | h | 102 | 100 | |
| deka | da | 101 | 10 | |
| — | — | 100 | 1 | — |
| deci | d | 10−1 | 0,1 | 1795 |
| centi | c | 10−2 | 0,01 | |
| mili | m | 10−3 | 0,001 | |
| mikro | μ | 10−6 | 0,000 001 | 1873 |
| nano | n | 10−9 | 0,000 000 001 | 1960 |
| piko | p | 10−12 | 0,000 000 000 001 | |
| femto | f | 10−15 | 0,000 000 000 000 001 | 1964 |
| atto | a | 10−18 | 0,000 000 000 000 000 001 | |
| zepto | z | 10−21 | 0,000 000 000 000 000 000 001 | 1991 |
| yokto | y | 10−24 | 0,000 000 000 000 000 000 000 001 | |
| ronto | r | 10−27 | 0,000 000 000 000 000 000 000 000 001 | 2022[43] |
| quecto | q | 10−30 | 0,000 000 000 000 000 000 000 000 000 001 | |
| ||||
Lexikografické konvence
Názvy jednotek
Podle příručky soustavy SI by se s názvy jednotek mělo zacházet jako s obecnými podstatnými jmény jazyka kontextu. To znamená, že by měly být psány ve stejné znakové sadě jako ostatní běžná podstatná jména (např. latinkou v češtině, cyrilicí v ruštině atd.) a měly by se řídit obvyklými gramatickými a pravopisnými pravidly kontextového jazyka. Například v češtině a angličtině, i když je jednotka pojmenována po osobě a její značka začíná velkým písmenem, by název jednotky v běžném textu měl začínat malým písmenem (např. newton, hertz, pascal) a píše se s velkým písmenem pouze na začátku věty a v nadpisech a názvech publikací. Jako netriviální aplikaci tohoto pravidla uvádí příručka, že název jednotky se značkou °C se správně píše jako „stupeň Celsia“: první písmeno názvu jednotky, „s“, se píše s malým písmenem, zatímco přívlastek „Celsius“ se píše s velkým písmenem, protože jde o vlastní jméno.[pozn. 18][1]:s.148
Značky jednotky a hodnoty veličin
Značky jednotek SI mají být jedinečné a univerzální, nezávislé na jazykovém kontextu.[16]:s.130–35 V příručce soustavy SI jsou uvedena specifická pravidla pro jejich zápis.[16]:s.130–35
Obecná pravidla pro zápis jednotek a veličin v soustavě SI se vztahují na text, který je buď psán rukou, nebo vytvořen automatizovaným postupem:
- Hodnota veličiny se zapisuje jako číslo, za kterým následuje mezera (představující znaménko násobení) a značka jednotky; např. 2,21 kg, 7,3×102 m2, 22 K. Toto pravidlo výslovně obsahuje znak procenta (%)[16]:s.134 a značku pro stupně Celsia (°C).[16]:s.133 Výjimkou jsou značky pro rovinné úhlové stupně, minuty a sekundy (°, ′ a ″), které se umísťují bezprostředně za číslo bez mezery.
- Značky jsou matematické entity, nikoli zkratky, a jako takové nemají připojenou tečku/úplnou tečku (.), pokud ji gramatická pravidla nevyžadují z jiného důvodu, například pro označení konce věty.
- Předpona je součástí jednotky a její značka je předřazena před značku jednotky bez oddělovače (např. k v km, M v MPa, G v GHz, μ v μg). Složené předpony nejsou povoleny. Jednotka s předponou je ve výrazech atomická (např. km2 je ekvivalentní (km)2).
- Značky jednotek se zapisují kolmým písmem (antikva) bez ohledu na typ použitý v okolním textu.
- Značky pro odvozené jednotky vzniklé násobením se spojují středovou tečkou (⋅) nebo nezlomitelnou mezerou; např. n⋅m nebo N m.
- Značky pro odvozené jednotky vytvořené dělením se spojují se lomítkem (/) nebo se uvádějí jako záporný exponent. Např. jednotku "metr za sekundu" lze zapsat jako m/s, m s−1, m⋅s−1 nebo . V případech, kdy za lomítkem následuje středová tečka (nebo mezera) nebo je přítomno více než jedno lomítko, je třeba použít závorky, aby se předešlo nejednoznačnosti. Například zápisy kg/(m⋅s2), kg⋅m−1⋅s−2 a (kg/m)/s2 jsou přijatelné, ale kg/m/s2 a kg/m⋅s2 jsou nejednoznačné a nepřijatelné.
- První písmeno značky jednotek odvozených od jména osoby se píše velkými písmeny, jinak se píší malými písmeny. Např. jednotka tlaku je pojmenována po Blaise Pascalovi, proto se její značka píše "Pa", ale značka pro mol se píše "mol". Takto je "T" značkou pro teslu, jednotku magnetické indukce, a "t" značkou pro tunu, jednotku hmotnosti. Od roku 1979 se litr může výjimečně psát buď s velkým, nebo s malým písmenem „L“, k čemuž vedla podobnost malého písmene „l“ s číslicí „1“, zejména v některých fontech.
- Značky nemají tvar množného čísla, např. 25 kg, nikoli 25 kgů.
- Velká a malá písmena předpon nejsou zaměnitelná. Např. veličiny 1 mW a 1 MW představují dvě různé veličiny (miliwatt a megawatt).
- Značkou pro desetinnou značku je buď čárka, nebo tečka na řádku. V praxi se v zemích kontinentální Evropy a ve většině Latinské Ameriky používá desetinná čárka a ve většině anglicky mluvících zemí a ve většině Asie se používá desetinná tečka.[45]
- Jako oddělovač tisíců (1 000 000) lze použít tenké mezery, aby se usnadnilo čtení, ale mezi skupiny tří číslic se nevkládají tečky ani čárky (1.000.000 nebo 1,000,000).[16]:s.133 Pokud jsou číslice pouze čtyři, mezera se obvykle nepoužívá k oddělení jedné číslice.
- Je třeba se vyhnout jakémukoli zalomení řádku uvnitř čísla, uvnitř složené jednotky nebo mezi číslem a jednotkou. Tam, kde to není možné, by se zlomy řádků měly shodovat s oddělovači tisíců.
- Vzhledem k tomu, že hodnota „bilion“ a „trilion“ se v různých jazycích liší, je třeba se vyhnout bezrozměrným výrazům „ppb“ (parts per billion) a „ppt“ (parts per trillion). Příručka soustavy SI nenavrhuje žádné alternativy.
Realizace jednotek
Metrologové pečlivě rozlišují mezi definicí jednotky a její realizací. Definice každé základní jednotky SI je sestavena tak, aby byla jedinečná a poskytovala spolehlivý teoretický základ, na němž lze provádět co nejpřesnější a nejreprodukovatelnější měření. Realizace definice jednotky je postup, kterým lze definici použít ke stanovení hodnoty a související nejistoty veličiny stejného druhu jako jednotka. Popis mise en pratique základních jednotek je uveden v elektronické příloze k příručce soustavy SI.[47][16]:s.168–169
Zveřejněná mise en pratique není jediným způsobem, jakým lze základní jednotku určit: v Příručce soustavy SI se uvádí, že "k realizaci libovolné jednotky SI lze použít jakoukoli metodu, která je v souladu s fyzikálními zákony".[16]:s.111
Definice vs. realizace jednotek
Od roku 2019 jsou veličiny všech jednotek SI definovány abstraktním způsobem, který je pojmově oddělen od jejich praktické realizace.[1]:s.126 Konkrétně jsou jednotky SI definovány stanovením, že sedm přírodních konstant SI[1]:s.125–129 má určité přesné číselné hodnoty, pokud jsou vyjádřeny v jednotkách SI. Pravděpodobně nejznámější z těchto konstant je rychlost světla ve vakuu c, která má v soustavě SI podle definice přesnou hodnotu c = 299 792 458 m/s. Dalších šest konstant je frekvence záření velmi jemného přechodu cesia ΔνCs, Planckova konstanta h, elementární náboj e, Boltzmannova konstanta k, Avogadrova konstanta NA a světelná účinnost Kcd. Povaha přírodních konstant sahá od základních přírodních konstant, jako je c, až po čistě technickou konstantu Kcd.[1]:s.128–129 Před rokem 2019 nebyly h, e, k a NA definovány a priori, ale jednalo se spíše o velmi přesně měřené veličiny. V roce 2019 byly jejich hodnoty definičně stanoveny na jejich nejlepší odhady v daném okamžiku, čímž byla zajištěna kontinuita s předchozími definicemi základních jednotek.
Co se týče realizace, to, co je považováno za současnou nejlepší praktickou realizaci jednotek, je popsáno v mises en pratique (francouzsky uvedení do praxe), které rovněž vydává BIPM.[48] Abstraktní povaha definic jednotek umožňuje zdokonalovat a měnit mises en pratique v závislosti na vývoji vědy a techniky, aniž by bylo nutné měnit samotné definice.
V jistém smyslu není tento způsob definice jednotek SI o nic abstraktnější než způsob, jakým se tradičně definují odvozené jednotky z hlediska základních jednotek. Vezměme si konkrétní odvozenou jednotku, například joule, jednotku energie. Její definice z hlediska základních jednotek je kg⋅m2/s2. I když jsou k dispozici praktické realizace metru, kilogramu a sekundy, praktická realizace joulu by vyžadovala nějaký odkaz na základní fyzikální definici práce nebo energie - nějaký skutečný fyzikální postup realizace energie v množství jednoho joulu tak, aby ji bylo možné porovnat s jinými případy energie (například s energií obsaženou v motorovém benzinu vpraveném do automobilu nebo v elektřině dodané do domácnosti).
Situace s definičními konstantami a všemi jednotkami SI je analogická. Čistě matematicky vzato jsou jednotky SI vlastně definovány tak, jako bychom prohlásili, že právě jednotky definiční konstanty jsou nyní základními jednotkami, přičemž všechny ostatní jednotky SI jsou jednotkami odvozenými. Abychom si to ujasnili, všimněme si nejprve, že každou definiční konstantu lze považovat za určující velikost měrné jednotky této definiční konstanty;[1]:s.128 například definice c definuje jednotku m/s jako 1 m/s = c / 299 792 458 ("rychlost jednoho metru za sekundu se rovná jedné 299 792 458 rychlosti světla"). Tímto způsobem definiční konstanty přímo definují následujících sedm jednotek:
- hertz (Hz), jednotka fyzikální veličiny frekvence;
- metr za sekundu (m/s), jednotka rychlosti;
- joule-sekunda (J⋅s), jednotka akce
- coulomb (C), jednotka elektrického náboje;
- joule na kelvin (J/K), jednotka entropie a tepelné kapacity;
- inverzní mol (mol-1), jednotka převodní konstanty mezi látkovým množstvím a počtem elementárních jednotek (atomů, molekul atd.);
- a lumen na watt (lm/W), jednotka světelné účinnosti (konstanta převodu mezi fyzikálním výkonem elektromagnetického záření a vlastní schopností tohoto záření vyvolat u člověka zrakový vjem jasu).
Dále lze pomocí rozměrové analýzy ukázat, že každou koherentní jednotku SI (ať už základní nebo odvozenou) lze zapsat jako jedinečný součin mocnin jednotek definičních konstant SI (zcela analogicky k tomu, že každou koherentní odvozenou jednotku SI lze zapsat jako jedinečný součin mocnin základních jednotek SI). Například kilogram lze zapsat jako kg = (Hz)(J⋅s)/(m/s)2. Kilogram je tedy definován v termínech tří definičních konstant ΔνCs, c a h, protože na jedné straně tyto tři definiční konstanty definují jednotky Hz, m/s, respektive J⋅s,[bm] na druhé straně lze kilogram zapsat v termínech těchto tří jednotek, a to kg = (Hz)(J⋅s)/(m/s)2. Ačkoli otázka, jak kilogram skutečně realizovat v praxi, by v tomto okamžiku byla stále otevřená, nijak se to neliší od skutečnosti, že otázka, jak skutečně realizovat joule v praxi, je v zásadě stále otevřená i poté, co jsme dosáhli praktické realizace metru, kilogramu a sekundy.
Určení základních konstant vs. jiné metody definice
Současný způsob definování SI je výsledkem desetiletí trvajícího směřování ke stále abstraktnějším a idealizovanějším formulacím, v nichž jsou realizace jednotek pojmově odděleny od definic.[1]:s.126
Velkou výhodou tohoto způsobu je, že s rozvojem vědy a technologií lze zavádět nové a dokonalejší realizace, aniž by bylo nutné jednotky znovu definovat. Jednotky lze nyní realizovat s přesností, která je v konečném důsledku omezena pouze kvantovou strukturou přírody a našimi technickými schopnostmi, nikoli však samotnými definicemi. K realizaci jednotky lze použít jakoukoli platnou fyzikální rovnici vztahující se k definičním konstantám, čímž se vytvářejí možnosti pro inovace… s rostoucí přesností s rozvojem technologií.[1]:s.122 V praxi poskytují poradní výbory CIPM takzvané "mises en pratique" (uvedení do praxe),[48] což jsou popisy toho, co se v současnosti považuje za nejlepší experimentální realizace jednotek.[49]
Tento systém postrádá koncepční jednoduchost používání etalonů (označovaných jako prototypy) jako realizací jednotek k definování těchto jednotek: u prototypů jsou definice a realizace jedno a totéž. Používání etalonů má však dvě zásadní nevýhody, které, jakmile je to technologicky a vědecky proveditelné, vedou k jejich opuštění jako prostředku k definování jednotek. Jednou z hlavních nevýhod je, že se artefakty mohou ztratit, poškodit nebo změnit. Druhou nevýhodou je, že z velké části nemohou využívat vědeckého a technologického pokroku. Posledním etalonem, který soustava SI používala, byl mezinárodní prototyp kilogramu, konkrétní válec z platiny a iridia; v letech 1889 až 2019 se kilogram z definice rovnal hmotnosti prototypu. Obavy týkající se jeho stability na jedné straně a pokrok v přesných měřeních Planckovy konstanty a Avogadrovy konstanty na straně druhé vedly k revizi definice základních jednotek, která vstoupila v platnost v květnu 2019.[50] Jednalo se o největší změnu v soustavě SI od jejího prvního formálního vymezení a zavedení v roce 1960, jejímž výsledkem jsou výše popsané definice.[51]
V minulosti existovaly i různé jiné přístupy k definicím některých jednotek SI. Jeden z nich využíval konkrétní fyzikální stav určité látky (trojný bod vody, který byl použit při definici kelvinu[16]:s.113–114); jiné odkazovaly na idealizované experimentální postupy[1]:s.125 (jako v případě dřívější definice ampéru v soustavě SI[16]:s.113 a dřívější definice kandely v soustavě SI (původně zavedené v roce 1979[16]:s.115).
V budoucnu může být soubor definičních konstant používaných soustavou SI upraven, pokud budou nalezeny stabilnější konstanty nebo pokud se ukáže, že jiné konstanty lze měřit přesněji.[pozn. 19]
Vedlejší jednotky
Mimosoustavové jednotky přijatelné pro použití s jednotkami SI
Ve vědecké, technické a komerční literatuře se nadále používá řada jednotek, které nejsou v souladu se standardem. Některé jednotky jsou hluboce zakořeněny v historii a kultuře a jejich používání nebylo zcela nahrazeno jejich alternativami v soustavě SI. CIPM uznal a potvrdil tyto tradice tím, že sestavil seznam jiných než SI, které jsou akceptovány pro použití se SI.[16]
Některé jednotky času, úhlu a starší jednotky, které nejsou jednotkami SI, mají dlouhou historii používání. Většina společností používala jako základ času sluneční den a jeho nedecimální dílčí jednotky, které byly na rozdíl od stopy nebo libry stejné bez ohledu na to, kde se měřily. Tuna, litr a hektar byly přijaty Generální konferencí pro míry a váhy v roce 1879 a byly zachovány jako jednotky, které lze používat vedle jednotek SI, a byly jim přiděleny jedinečné značky. Katalogizované jednotky jsou uvedeny níže.
Většina z nich vyžaduje pro převod na odpovídající jednotku SI převodní koeficienty, které nejsou mocninami deseti. Mezi běžné příklady takových jednotek patří běžné jednotky času, konkrétně minuta (převodní faktor 60 s/min, protože 1 min = 60 s), hodina (3600 s) a den (86400 s); stupeň (pro měření úhlů, 1° = π/180 rad) a elektronvolt (jednotka energie, 1 eV = 1,602176634×10−19 J).
| Veličina | Jednotka | Značka jednotky | Převod na jednotky SI |
|---|---|---|---|
| čas | minuta | min | 1 min = 60 s |
| hodina | h | 1 h = 60 min = 3600 s | |
| den | d | 1 d = 24 h = 86 400 s | |
| délka | astronomická jednotka | au | 1 au = 149 597 870 700 m |
| úhel | úhlový stupeň | ° | 1° = rad |
| úhlová minuta | ′ | 1′ = (1/60)° = rad | |
| (úhlová) vteřina | ″ | 1″ = (1/60)′ = rad | |
| plošný obsah | hektar | ha | 1 ha = 1 hm2 = 104 m2 |
| objem | litr | l, L | 1 l = 1 L = 1 dm3 = 103 cm3 = 10−3 m3 |
| hmotnost | tuna | t | 1 t = 103 kg |
| dalton | Da | 1 Da = 1,660 539 066 60(50)×10−27 kg | |
| energie | elektronvolt | eV | 1 eV = 1,602 176 634×10−19 J |
| logaritmické veličiny pro poměr | neper | Np | bezrozměrné jednotky vyjadřující logaritmus poměru dvou hodnot |
| bel | B | ||
| decibel | dB |
Metrické jednotky, které soustava SI neuznává
Ačkoli se termín metrická soustava často používá jako neformální alternativní název pro Mezinárodní soustavu jednotek,[52] existují i jiné metrické soustavy, z nichž některé se v minulosti hojně používaly nebo se dokonce v určitých oblastech stále používají. Existují také jednotlivé metrické jednotky, například sverdrup a darcy, které existují mimo jakoukoli soustavu jednotek. Většinu jednotek jiných metrických soustav soustava SI neuznává.[pozn. 20][pozn. 21]
Příkladem je soustava centimetr-gram-sekunda (CGS), která byla dominantním metrickou soustavou ve fyzikálních vědách a elektrotechnice od 60. let 19. století přinejmenším do 60. let 20. století a v některých oborech se stále používá. Ve oblasti mechaniky používá takové v SI neuznávané jednotky jako gal, dyne, erg, barye atd. a v dynamice tekutin poise a stokes. Pokud jde o jednotky veličin v elektřině a magnetismu, existuje několik verzí soustavy CGS. Dvě z nich jsou zastaralé: elektrostatická soustava CGS ("CGS-ESU", s jednotkami neuznávanými v soustavě SI statcoulomb, statvolt, statampér atd.) a elektromagnetická soustava CGS ("CGS-EMU", s jednotkami abampér, abcoulomb, oersted, maxwell, abhenry, gilbert atd. Směs těchto dvou soustav je stále populární a je známá jako Gaussova soustava (která obsahuje gauss jako zvláštní název pro jednotku CGS-EMU maxwell na centimetr čtvereční).
Ve strojírenství (kromě elektrotechniky) mělo dříve dlouhou tradici používání gravitační metrické soustavy, k jejímž SI neuznávaným jednotkám patří kilogram síly (kilopond), technická atmosféra, metrická koňská síla atd. V Sovětském svazu se v letech 1933 až 1955 používala soustava metr-tuna-sekunda (mts), která měla takové v soustavě SI neuznávané jednotky, jako je stén, pièze atd. Dalšími skupinami metrických jednotek neuznávaných v soustavě SI jsou různé starší jednotky a jednotky CGS týkající se ionizujícího záření (rutherford, curie, rentgen, rad, rem atd. ), radiometrie (langley, jansky), fotometrie (phot, nox, stilb, nit, metrová svíčka,[53]:17 lambert, apostilb, skot, brill, troland, talbot, desetinná svíčka, candle), termodynamiky (kalorie) a spektroskopie (reciproký centimetr).
Mezi další neuznávané metrické jednotky SI, které nespadají do žádné z již zmíněných kategorií, patří například ar, bar, barn, fermi, grad (gon, gradián), metrický karát, mikron, milimetr rtuti, torr, milimetr (nebo centimetr či metr) vody, milimikron, mho, stere, jednotka x, γ (jednotka hmotnosti), γ (jednotka hustoty magnetického toku) a λ (jednotka objemu).[54]:s.20–21 V některých případech mají metrické jednotky neuznávané v SI ekvivalentní jednotky SI vytvořené kombinací metrické předpony a koherentní jednotky SI. Například 1 γ (jednotka hustoty magnetického toku) = 1 nT, 1 Gal = 1 cm⋅s-2, 1 barye = 1 deci pascal atd (příbuznou skupinou jsou korelace, jako 1 abampér ≘ 1 deka ampér, 1 abhenry ≘ 1 nanohenry atd). Někdy nejde ani o metrickou předponu: jednotka neuznávaná v SI může být úplně stejná jako koherentní jednotka SI, až na to, že SI neuznává speciální název a značka. Například nit je pouze SI-neuznávaný název pro jednotku SI kandela na metr čtvereční a talbot je SI-neuznávaný název pro jednotku SI lumen sekunda. Často je metrická jednotka, která není součástí SI, vztažena k jednotce SI sice prostřednictvím mocniny desítky, ale ne jednotky s metrickou předponou, např. 1 dyn = 10−5 newtonů, angström (1 Å = 10−10 m), který se stále používá v různých oborech, atd. (a korelace jako 1 gauss ≘ 10−4 tesla). A konečně existují metrické jednotky, jejichž převodní koeficienty na jednotky SI nejsou mocninami deseti, např. 1 kalorie = 4,184 joulu a 1 kilogram síly = 9,806650 newtonu. Některé metrické jednotky neuznávané v SI se stále často používají, např. kalorie (ve výživě), rem (v USA), jansky (v radioastronomii), gauss (v průmyslu) a obecněji CGS-Gausovy jednotky (v některých podoborech fyziky), metrická koňská síla (pro výkon motoru v řadě neanglicky mluvících zemí), kilogramová síla (pro tah raketových motorů, v Číně a někdy i v Evropě) atd. Jiné se dnes používají jen zřídka, například sthene a rutherford.
Nepřijatelná použití
Někdy se zavádějí varianty názvů jednotek SI, které směšují informace o příslušné fyzikální veličině nebo podmínkách jejího měření; tato praxe je však u soustavy SI nepřijatelná. Mezi příklady patří např: "watt-peak" a "watt RMS"; "geopotenciální metr" a "vertikální metr"; "standardní metr krychlový"; "atomová sekunda", "efemeridová sekunda" a "hvězdná sekunda".
Historické souvislosti
V průběhu Velké francouzské revoluce (1789–1799) vznikla potřeba redefinice do té doby používaných různých jednotek, v roce 1790 proto Ústavodárné shromáždění pověřilo vědeckou komisi ve stanovením soustavy jednotek a dne 18. germinalu r. III (7. dubna 1795) stanovilo povinnost používání nového „absolutního systému metrických jednotek“ od 2. listopadu 1801. Napoleon Bonaparte sice svým dekretem 12. února 1812 znovu povolil staré jednotky, ale nový zákon ze dne 4. července 1837 povinnost používat metrickou soustavu ve Francii opět zavedl od 1. ledna 1840 a díky tomu, že ji francouzské vlády neustále propagovaly, nabývala tato soustava na mezinárodní oblibě a 25. května 1875 podepsali zástupci osmnácti zemí tzv. Metrickou konvenci, která mj. založila Mezinárodní úřad pro míry a váhy, spravovaný mezinárodním výborem. Například v Rakousko-Uhersku byla metrická soustava zavedena zákonem ze dne 23. července 1871 s platností od 1. ledna 1876.
Jako základ jednotek délky byl tehdy navržen metr coby zemského kvadrantu a na základě dekretu ze dne 10. prosince 1799 byl zhotoven etalon metru (nejprve mosazný, poté platinový), který byl nazván archivním metrem. Podle něj pak byl vyroben mezinárodní etalon metru (ze slitiny platiny a iridia) a jeho kopie byly vydány členským státům konvence.

Původní systém mezinárodní jednotek, používaný zhruba od roku 1874, byl definován jako soustava CGS (centimetr-gram-sekunda), která ale měla řadu odvozenin a modifikací pro některé vědní obory. Proto byla poměrně brzo redefinována a v roce 1889 tak vznikla Soustava MKS (metr-kilogram-sekunda). S postupujícím rozvojem vědy a techniky však vyvstávala potřeba definovat a mezinárodně normalizovat další fyzikální jednotky. Od roku 1921 se datují přípravy této nové soustavy, v roce 1948 začal mezinárodní standardizační proces. Například v tehdejším Československu se tak stalo zákonem č. 35/1962 Sb. ze dne 29. 3. 1962, o měrové službě.[55]
Mezinárodní výbor pro míry a váhy navrhl v roce 2011 změnu definic základních jednotek soustavy SI,[56][57] která byla přijatá v roce 2018 a vstoupila v platnost v květnu 2019. Sada sedmi základních jednotek jako takových zůstala zachována: metr, kilogram, sekunda, kelvin, ampér, kandela a mol. Staré definice sekundy, metru a kandely byly považovány za vyhovující, a proto se změnily jen jejich formulace s ohledem na jednotný formát pro všechny jednotky. Definice kilogramu, ampéru, kelvinu a molu byly ale principiálně změněny tak, že každá z těchto jednotek je pevně spjata s určitou neměnnou vlastností přírody. Důležitým požadavkem na nové definice byla samozřejmě zpětná kompatibilita, tedy aby nové jednotky byly stejně velké jako stávající s maximální dosažitelnou přesností.
Relativita
Jednotky SI jsou s ohledem na teorii relativity realizovány podle svých definic lokálně jako vlastní jednotky (veličin jako je vlastní čas, vlastní délka, vlastní hmotnost atd.).[17]:s.30, 141–142
Soustava SI v České republice
V České republice stanovuje povinnost používat soustavu jednotek SI zákon č. 505/1990 Sb. o metrologii (ve znění zákona č. 152/2021 Sb.) a prováděcí vyhláška č. 424/2009 Sb., kterou se mění vyhláška Ministerstva průmyslu a obchodu č. 264/2000 Sb., o základních měřicích jednotkách a ostatních jednotkách a o jejich označování. Těmito předpisy je také stanoven Český metrologický institut jako garant jednotek a etalonů pro Českou republiku.
Definice, doporučené značení základních a odvozených veličin, jejich jednotky a jejich závazné značky jsou v České republice upraveny normami řady ČSN ISO IEC 80000 „Veličiny a jednotky“, která nahradila předchozí řadu ČSN ISO 31 (z roku 1992) stejného názvu, taktéž založenou na SI.
Odkazy
Poznámky
- ↑ Z francouzského: Conférence générale des poids et mesures.
- ↑ a b Například newton (N), jednotka síly, je ekvivalentní s kg⋅m⋅s−2; joule (J), jednotka energie, je ekvivalentí s kg⋅m2⋅s−2, atd. Nejnověji pojmenovaná odvozená jednotka, katal, byla definována v roce 1999.
- ↑ To znamená, že různé jednotky pro danou veličinu, například délku, jsou spojeny pomocí činitele 10. Výpočty proto zahrnují jednoduchý proces posunu desetinné čárky doprava nebo doleva.[8]
- ↑ Ačkoli se pojmy metrický systém a SI často používají jako synonyma, ve skutečnosti existuje mnoho vzájemně nekompatibilních metrických systémů. Navíc existují metrické jednotky, které nejsou uznávány žádnou větší metrickou soustavou.
- ↑ Mezi americkou běžnou soustavou Spojených států a imperiálním systémem Spojeného království existují rozdíly. Například imperiální galon je asi o 20 % větší než americký galon.
- ↑ A jsou definovány v termínech metrických předchůdců soustavy SI přinejmenším od 90. let 19. století.
- ↑ K dubnu 2020 mezi ně patřily ty ze Španělska (CEM), Ruska (FATRiM), Švýcarska (METAS), Itálie (INRiM), Jižní Koreje (KRISS), Francie (LNE), Číny (NIM), USA (NIST), Japonsko (AIST/ NIMJ), Spojené království (NPL), Kanada (NRC) a Německo (PTB).
- ↑ Z historických důvodů se za koherentní jednotku považuje kilogram, nikoli gram, což představuje výjimku z této charakteristiky.
- ↑ Legislativní překlad je v ústřední pasáži formulován fyzikálně nesprávně. Originální definice nesouvisí s četností/frekvencí daného přechodu, ale jedná se o frekvenci (elektromagnetického) záření, které by bylo vysláno při přechodu elektronu atomového obalu cesia mezi stavy s danými energetickými hladinami, odpovídající rozdílu jejich energií podle vztahu ΔE=hν. Fyzikálně korektnější formulace by zněla „… frekvence ΔνCs odpovídající přechodu …“ či „… frekvence ΔνCs záření při přechodu …“ (v obou případech bez vložené interpunkční čárky). Také značka dané konstanty je poněkud zavádějící, neboť se nejedná o rozdíl frekvencí.
- ↑ Jednoelektronové pumpy s laditelným taktováním se realizují polovodičovými přechody[24] nebo tzv. hybridními elektronickými turnikety využívajícími přechodu mezi normální a supravodivou fází. Nejpřesnějším typem jsou pumpy s metalickými ostrůvky, využívající tunelový jev přes přechodovou bariéru; jsou však natolik pomalé, že pro proudový etalon jsou nevyhovující. V roce 2013 se při spolupráci britských výzkumných týmů NPL a Cavendishovy laboratoře podařilo vytvořit jednoelektronovou pumpu na bázi grafenu, který má chování podobné kovu, a přitom umožňuje rychlý průchod elektronů pumpou. Přitom může být dosaženo frekvence řádu gigahertzů, požadované pro proudový etalon. Stala se tak nejvýznamnějším současným kandidátem na přímou realizaci nově definovaného ampéru.[25][26]
- ↑ Zde je několik příkladů souvislých odvozených jednotek SI: jednotka rychlosti, což je metr za sekundu, se značkou m/s; jednotka zrychlení, což je metr za sekundu na druhou, se značkou m/s2; atd.
- ↑ a b Z historických důvodů se názvy a značky pro desetinné násobky a díly jednotky hmotnosti tvoří, jako by základní jednotkou byl gram, tj. připojením předponových názvů a značek k názvu jednotky "gram" a značky jednotky "g". Například 10−6 kg se zapisuje jako miligram, mg, nikoli jako mikrokilogram, μkg.[1]{:s.144
- ↑ Jak uvádí příručka soustavy SI,[1]:s.140. to platí nejen pro technické texty, ale také například pro měřicí přístroje (tj. na displeji přístroje musí být uvedena jak jednotka, tak měřená veličina).
- ↑ Obvykle se však srážky měří v nekoherentních jednotkách SI, jako jsou milimetry srážek na každém metru čtverečním za určité období, což odpovídá litrům na metr čtvereční.
- ↑ Je správné říci, že základní jednotka SI (např. metr) je koherentní jednotkou pro odpovídající fyzikální veličinu. Připomeňme, že soubor koherentních jednotek SI se skládá ze základních jednotek a koherentních odvozených jednotek. Toto použití je v souladu s definicí koherentní jednotky jako jednotky, která je rovna "součinu mocnin základních jednotek s předčinitelem 1". Ostatně každá základní jednotka je zjevně takto reprezentovatelná - je rovna sama sobě s mocninou 1 a s prefaktorem 1.
- ↑ Jinými slovy, vzhledem k jakékoli základní jednotce nebo jakékoli souvislé odvozené jednotce se speciálním názvem a značkou.
- ↑ Toto poslední tvrzení se ve skutečnosti vztahuje na "všechny" jednotky SI, nejen na jednotky se speciálními názvy a značkami. Vezměme si příklad jednotek SI pro točivý moment. Protože SI nemá jednotku se speciálním názvem a značkou pro točivý moment, je její koherentní jednotkou SI newtonmetr, N⋅m. Níže jsou uvedeny některé příklady nekoherentních jednotek točivého momentu SI: N⋅mm, kN⋅μm, mN⋅cm, etc. Všimněte si, že tyto nekoherentní jednotky se získávají z původní koherentní jednotky nahrazením některých (nebo všech) jednotek se speciálními názvy a značkami, které se vyskytují v původní koherentní jednotce, jejich desetinnými násobky nebo díly. Tyto různé mocniny deseti se pak ale spojí do jedné celkové mocniny deseti. Např. kN⋅μm = (103 N)⋅(10−6 m) = 103–6 N⋅m = 10−3 N⋅m.
- ↑ Jednotka je pojmenována podle Anderse Celsia.
- ↑ Jak bylo uvedeno výše, je téměř jisté, že definiční konstanta bude muset být relativně brzy nahrazena, protože je stále jasnější, že přesnější časové standardy mohou poskytnout jiné atomy než cesium. Není však vyloučeno, že některé z dalších definičních konstant budou muset být časem nahrazeny také. Například elementární náboj e} odpovídá síle vazby elektromagnetické síly prostřednictvím konstanty jemné struktury . Některé teorie předpovídají, že se může v čase měnit. V současnosti známé experimentální limity maximální možné změny jsou tak nízké, že "jakýkoli vliv na předvídatelná praktická měření lze vyloučit",[1]:s.128 i kdyby se jedna z těchto teorií ukázala jako správná. Nicméně pokud se ukáže, že se konstanta jemné struktury v čase mírně mění, může věda a technika v budoucnu pokročit natolik, že se takové změny stanou měřitelnými. V té chvíli by bylo možné uvažovat o tom, že pro účely definice SI nahradíme elementární náboj nějakou jinou veličinou, jejíž volba bude záviset na tom, co se dozvíme o změnách v čase.
- ↑ To znamená, že nejsou ani součástí soustavy SI, ani jednou z jednotek, které sice nejsou součástí této soustavy, ale které jsou s touto soustavou přijímány.
- ↑ Navíc některé jednotky jsou uznávány ve všech metrických systémech. Sekunda je základní jednotkou ve všech z nich. Metr je ve všech uznáván buď jako základní jednotka délky, nebo jako desetinný násobek či díl základní jednotky délky. Naproti tomu ne každá metrická soustava uznává gram jako jednotku (buď jako základní jednotku, nebo jako desetinný násobek základní jednotky). Zejména v gravitačních metrických soustavách nahrazuje jednotka síly (gram-síla nebo kilogram-síla) jednotku hmotnosti jako základní jednotku. Jednotka hmotnosti je pak odvozenou jednotkou, definovanou jako hmotnost, která je při působení čisté jednotkové síly urychlována jednotkovou rychlostí (tj. rychlostí 1 základní délkové jednotky (téměř vždy buď metr, nebo centimetr) za sekundu na druhou).
Reference
V tomto článku byl použit překlad textu z článku International System of Units na anglické Wikipedii.
- ↑ a b c d e f g h i j k l m n o p q r s t u v w x y z aa International Bureau of Weights and Measures. The International System of Units (SI) [online]. 9. vyd. 2019-05-20. Dostupné online. ISBN 978-92-822-2272-0.
- ↑ Předpony přijaté před rokem 1960 existovaly již před SI. Soustava CGS byla zaveden v roce 1873.
- ↑ CROWDER, Stephen; DELKER, Collin; FORREST, Eric; MARTIN, Nevin. Introduction to Statistics in Metrology. [s.l.]: Springer Nature, 30 November 2020. Dostupné online. ISBN 978-3-030-53329-8. (anglicky)
- ↑ MAGAZINE, Smithsonian; ESCHNER, Kat. America Has Been Struggling With the Metric System For More Than 200 Years [online]. 27 July 2017. Dostupné v archivu pořízeném z originálu dne 26 August 2021. (anglicky)
- ↑ CURTIN, Kevin M. Encyclopedia of World Geography. Distance. Redakce McColl R. W.. New York, NY: Facts on File, an imprint of Infobase Publishing, 14 May 2014. ISBN 978-0-8160-7229-3. (anglicky)
- ↑ The measure of all things [online]. National Physical Laboratory, UK [cit. 2021-10-07]. Dostupné v archivu pořízeném z originálu dne 28 November 2020. (anglicky)
- ↑ a b Interpretation of the International System of Units (the Metric System of Measurement) for the United States. Federal Register. National Institute of Standards and Technology, 16 May 2008, s. 28432. Dostupné v archivu pořízeném z originálu dne 16 August 2017.
- ↑ The United States and The Metric System (A Capsule History). Gaithersburg, MD, USA: NIST, 1997. Dostupné v archivu pořízeném z originálu dne 16 April 2020. S. 2.
- ↑ Member States [online]. BIPM, 2021 [cit. 2021-10-19]. Dostupné v archivu pořízeném z originálu dne 19 October 2021.
- ↑ The role of the Consultative Committees [online]. BIPM, 2014 [cit. 2020-04-18]. Dostupné v archivu pořízeném z originálu dne 4 February 2020.
- ↑ Consultative Committee for Units (CCU) [online]. BIPM, 2006 [cit. 2020-04-18]. Dostupné v archivu pořízeném z originálu dne 31 January 2020.
- ↑ Consultative Committee for Units (CCU): Criteria for membership [online]. BIPM, 2006 [cit. 2020-04-18]. Dostupné v archivu pořízeném z originálu dne 2 July 2019.
- ↑ Consultative Committee for Units (CCU): Members [online]. BIPM, 2006 [cit. 2020-04-18]. Dostupné v archivu pořízeném z originálu dne 2 July 2019.
- ↑ Welcome - BIPM [online]. Dostupné online.
- ↑ a b c d e The International System of Units (SI). Redakce David B. Newell. NIST Special publication 330, 2019. vyd. Gaithersburg, MD: NIST, 2019. Dostupné online.
- ↑ a b c d e f g h i j k l m n o International Bureau of Weights and Measures. The International System of Units (SI) [online]. 8. vyd. 2006 [cit. 2021-12-16]. Dostupné online. ISBN 92-822-2213-6.
- ↑ a b c d Bureau international des poids et mesures. Le Système international d’unités (SI) – The International System of Units (SI) [PDF]. 9. vyd. 2019 [cit. 2021-12-20]. Dostupné online. ISBN 978-92-822-2272-0. (francouzsky, anglicky)
- ↑ Zákon č. 152/2021 Sb., kterým se mění zákon č. 505/1990 Sb., o metrologii, ve znění pozdějších předpisů. [cit. 2021-12-20]. Dostupné online.
- ↑ MATERESE, Robin. Historic Vote Ties Kilogram and Other Units to Natural Constants. NIST. 16 November 2018. Dostupné online [cit. 16 November 2018].
- ↑ Rozhodnutí č. 9 jedenácté Generální konference pro míry a váhy Archivováno 19. 3. 2021 na Wayback Machine. (1960)
- ↑ CCTF Strategy Document, květen 2016. Dostupné online (PDF) (anglicky)
- ↑ RIEHLE, Fritz; GILL, Patrick; ARIAS, Felicitas; ROBERTSSON, Lennart. The CIPM list of recommended frequency standard values: guidelines and procedures. Kapitola 5. Towards a new definition of the SI second, s. 196–197. Metrologia [online]. IOP Publishing, 14. únor 2018. Svazek 55, čís. 2, s. 196–197. Dostupné online. PDF [1]. ISSN 1681-7575. doi:10.1088/1681-7575/aaa302. (anglicky)
- ↑ Rozhodnutí č. 6 jedenácté Generální konference pro míry a váhy (1960). www.bipm.org [online]. [cit. 2020-06-23]. Dostupné v archivu pořízeném z originálu dne 2020-06-20.
- ↑ GIBLIN, S. P.; BAE, M.-H.; AHN, Ye-Hwan; KATAOKA, M. Robust operation of a GaAs tunable barrier electron pump. S. 299–306. Metrologia [online]. BIPM & IOP Publishing Ltd., 5. březen 2017. Svazek 54, čís. 3, s. 299–306. Dostupné online. ISSN 1681-7575. doi:10.1088/1681-7575/aa634c. (anglicky)
- ↑ CONNOLLY, M. R., CHIU, K. L.; GIBLIN, S. P.; KATAOKA, M.; FLETCHER, J. D.; CHUA, C.; GRIFFITHS, J. P.; JONES, G. A. C.; FAĽKO, V. I.; SMITH, C. G.; JANSSEN T. J. B. M. Gigahertz quantized charge pumping in graphene quantum dots. S. 417–420. Nature Nanotechnology [online]. 12. květen 2013. Svazek 8, čís. 6, s. 417–420. Dostupné online. PDF [2]. ISSN 1748-3395. doi:10.1038/nnano.2013.73. (anglicky)
- ↑ DUMÉ, Belle: Redefining the ampere with the help of graphene? Physics.World.com, 28. květen 2013. Dostupné online (anglicky)
- ↑ Rozhodnutí č. 3 třinácté Generální konference pro míry a váhy (1967). www.bipm.org [online]. [cit. 2020-06-23]. Dostupné v archivu pořízeném z originálu dne 2020-05-08.
- ↑ Rozhodnutí č. 4 třinácté Generální konference pro míry a váhy (1967). www.bipm.org [online]. [cit. 2020-06-23]. Dostupné v archivu pořízeném z originálu dne 2007-06-15.
- ↑ Rozhodnutí č. 3 čtrnácté Generální konference pro míry a váhy (1971). www.bipm.org [online]. [cit. 2020-06-23]. Dostupné v archivu pořízeném z originálu dne 2021-03-04.
- ↑ Rozhodnutí č. 6 desáté Generální konference pro míry a váhy Archivováno 22. 6. 2020 na Wayback Machine. (1954)
- ↑ Rozhodnutí č. 5 třinácté Generální konference pro míry a váhy Archivováno 26. 9. 2020 na Wayback Machine. (1954)
- ↑ Rozhodnutí č. 3 šestnácté Generální konference pro míry a váhy Archivováno 21. 3. 2020 na Wayback Machine. (1979)
- ↑ Units & Symbols for Electrical & Electronic Engineers [online]. Institution of Engineering and Technology, 1996 [cit. 2013-08-19]. S. 8–11. Dostupné v archivu pořízeném z originálu dne 28 June 2013.
- ↑ ATKINS, Tony; ESCUDIER, Marcel. A Dictionary of Mechanical Engineering. [s.l.]: Oxford University Press, 2019. ISBN 9780199587438. OCLC 1110670667
- ↑ CHAPPLE, Michael. Dictionary of Physics. [s.l.]: Taylor & Francis, 2014. ISBN 9781135939267. OCLC 876513059
- ↑ Earth now weighs six ronnagrams: New metric prefixes voted in [online]. phys.org, 18 November 2022. Dostupné online.
- ↑ List of Resolutions for the 27th meeting of the General Conference on Weights and Measures [online]. 18 November 2022 [cit. 2022-11-18]. Dostupné v archivu pořízeném z originálu dne 18 November 2022.
- ↑ 2022-12-19-si-prefixes - BIPM [online]. [cit. 2023-01-11]. Dostupné online.
- ↑ Decimal Nature of the Metric System [online]. US Metric Association, 2015 [cit. 2020-04-15]. Dostupné v archivu pořízeném z originálu dne 15 April 2020.
- ↑ THOMPSON, Ambler; TAYLOR, Barry N. Guide for the Use of the International System of Units (SI) (Special publication 811). Gaithersburg, MD: National Institute of Standards and Technology, 2008. Dostupné online.
- ↑ Bureau International des Poids et Mesures. Le Système international d’unités (SI) – The International System of Units (SI) [online]. 8. vyd. Paris: STEDI MEDIA, květen 2006. Kapitola 3.1, s. 32, 121. Dostupné online. ISBN 92-822-2213-6. (francouzsky, anglicky)
- ↑ HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fyzika. Brno, Praha: Vysoké učení technické v Brně – Nakladatelství VUTIUM a PROMETHEUS, 2001. ISBN 80-214-1868-0. Kapitola 1.3, s. 3.
- ↑ a b On the extension of the range of SI prefixes [online]. 18 November 2022 [cit. 2023-02-05]. Dostupné online.
- ↑ Metric (SI) Prefixes [online]. NIST. Dostupné online.
- ↑ WILLIAMSON, Amelia A. Period or Comma? Decimal Styles over Time and Place. Science Editor. March–April 2008, s. 42. Dostupné v archivu pořízeném z originálu dne 28 February 2013.
- ↑ Avogadro Project [online]. National Physical Laboratory [cit. 2010-08-19]. Dostupné online.
- ↑ What is a mise en pratique? [online]. International Bureau of Weights and Measures [cit. 2012-11-10]. Dostupné online.
- ↑ a b Practical realizations of the definitions of some important units [online]. BIPM, 2019 [cit. 2020-04-11]. Dostupné v archivu pořízeném z originálu dne 9 April 2020.
- ↑ What is a mise en pratique? [online]. BIPM, 2011 [cit. 2015-09-06]. Dostupné v archivu pořízeném z originálu dne 22 September 2015.
- ↑ MATERESE, Robin. Historic Vote Ties Kilogram and Other Units to Natural Constants. NIST. 16 November 2018. Dostupné online [cit. 16 November 2018].
- ↑ Kilogram finally redefined as world's metrologists agree to new formulation for SI units [online]. 16 November 2018 [cit. 2020-09-19]. Dostupné online. (anglicky)
- ↑ OLTHOFF, Jim. For All Times, For All Peoples: How Replacing the Kilogram Empowers Industry. NIST. 2018. Dostupné v archivu pořízeném z originálu dne 16 March 2020.
- ↑ TROTTER, Alexander Pelham. Illumination: Its Distribution and Measurement. London: Macmillan, 1911. OCLC 458398735
- ↑ IEEE/ASTM SI 10 American National Standard for Use of the International System of Units (SI): The Modern Metric System. [s.l.]: IEEE and ASTM, 2016.
- ↑ Zákon č. 35/1962 Sb., o měrové službě. [cit. 2021-12-20]. Dostupné online.
- ↑ On the possible future revision of the International System of Units, the SI; Draft Resolution A; dostupné online
- ↑ Draft Chapter 2 for SI Brochure, following redefinitions of the base units. dostupné online
Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu Soustava SI na Wikimedia Commons
Obrázky, zvuky či videa k tématu Soustava SI na Wikimedia Commons  Slovníkové heslo SI ve Wikislovníku
Slovníkové heslo SI ve Wikislovníku- Český metrologický institut
- Mezinárodní úřad pro míry a váhy
Média použitá na této stránce
Autor: Dono, Licence: CC BY-SA 3.0
The seven SI base units and their interdependency. Clockwise from the top: second (time), kilogram (mass), mole (amount of substance), candela (luminous intensity), Kelvin (temperature), Ampere (electric current) and metre (distance)
(c) Goran tek-en, CC BY-SA 4.0
Countries using the metric, US customary and imperial systems of units as of 2019. Only the USA uses the US customary system; Liberia, Samoa, Palau, Micronesia, and Marshall Islands use unknown (i.e. it is unclear which system they use) non-metric systems; it is impossible to clearly determine which system Myanmar uses; the UK and Canada use a mixture of imperial and metric systems.
A national prototype kilogram standard mass, number K4, kept by the National Institute of Standards and Technology, USA, one of two which serve as the official standard for defining all units of weight and mass in the United States. It is a polished cylinder made of 90% platinum - 10% iridium alloy, 39 mm (1.5 inches) in diameter and 39 mm high. It is an exact copy of the international prototype kilogram kept at the International Bureau of Weights and Measures (Bureau International des Poids et Measures) in Sevres, France It was one of 40 copies which were presented by France in 1884 to different nations as national standards. This copy, K4, serves as a secondary comparison standard, while its twin, K20, serves as the primary standard. In 1884, it differed in mass from the prototype kilogram by about 75 micrograms. Alterations to image: Removed aliasing artifacts (stripes) due to scanning of halftone photo using GIMP FFT filter.
Autor:
- Cube.svg: Image created by H McKenna based on source code by Marcelo Reis.
- derivative work: Cristianrodenas (talk)
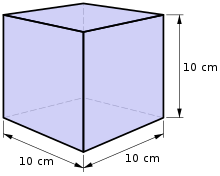
Litre definition as the volume of a cube measuring 10cm each edge.
Autor: Japs 88, Licence: CC BY-SA 3.0
A replica of the prototype of the kilogram at the Cité des Sciences et de l’Industrie, Paris, France.
(c) The Commonwealth Scientific and Industrial Research Organisation of Australia, CC BY-SA 3.0
A 1-kg single-crystal silicon sphere for the Avogadro Project is shown above in the hands of Master Optician Achim Leistner at the Australian Centre for Precision Optics (ACPO), which is part of Australia's Commonwealth Scientific and Industrial Research Organisation (CSIRO).
ACPO's spheres are among the roundest man-made objects on Earth. (The gyroscopes of Gravity Probe B are equally round but are in orbit, not "on Earth".) If one of their Ø 93.6 mm spheres, which had an out-of-roundness of 35 nm, was scaled to the size of the Earth, its ‘continents’ would gradually rise only 2.4 meters above sea level.
Computer generated image of International Prototype Metre bar, made of 90% platinum - 10% iridium alloy. This was the standard of length for the SI (Metric system) from 1889 until 1960, when the SI system changed to a new definition of length based on the wavelength of light emitted by krypton 86. The length of the metre was defined by the distance between two fine lines ruled on the central rib of the bar near the ends, at the temperature of freezing water. The bar was given an X (Tresca) cross-sectional shape to increase its stiffness-to-weight ratio, improve its thermal accommodation time, and so the graduation lines could be located on the "neutral" axis of the bar where the change in length with flexure is minimum. The prototype was made in 1889, its length made equal to the previous French standard "Metre of the Archives". Twenty-nine identical copies were made at the same time, which were calibrated against the prototype and distributed to nations to serve as national standards.
The main problem with defining the unit of length by an artifact such as a bar is that there is no foolproof way of detecting a change in its length due to age or misuse. It can be compared to other copies, but these themselves may have changed in length. This motivated the 1960 change to a definition based on light waves. The bar is now kept in the collection of the BIPM museum.