Soustava lineárních rovnic

V matematice se soustavou lineárních rovnic označuje systém jedné nebo více lineárních rovnic se společnými neznámými.

Příkladem soustavy tří lineárních rovnic o třech neznámých je:

${\displaystyle {\begin{array}{rcrcrcr}3x&+&2y&-&z&=&1\\2x&-&2y&+&4z&=&-2\\-x&+&{\frac {1}{2}}y&-&z&=&0\end{array}}}$

Jsou-li neznámým proměnným přiřazeny hodnoty tak, že všechny rovnice soustavy platí zároveň, nazývá se tato volba hodnot řešením soustavy. V naší ukázce je řešením uspořádaná trojice ${\displaystyle (x,y,z)=(1,-2,-2)}$, protože splňuje všechny tři rovnice současně. Slovo „soustava“ naznačuje, že podmínky dané rovnicemi je třeba splnit najednou, nikoli jen některé.

Soustava lineárních rovnic je ústřední pojem lineární algebry, oboru, který je používán ve mnoha oblastech moderní matematiky. Algoritmy pro nalezení řešení jsou důležitou součástí numerické lineární algebry.

Důležitost této oblasti matematiky spočívá v tom, že fyzikální modely bývají metodou konečných prvků nebo metodou konečných diferencí převáděny na úlohy s obrovskými soustavami lineárních rovnic. Proto hrají metody pro práci s těmito rovnicemi a algoritmy pro řešení těchto rovnic významnou roli ve strojírenství, fyzice, chemii, informatice a ekonomii.

Soustava nelineárních rovnic může být často aproximována lineární soustavou rovnic (viz lineární aproximace), což je užitečná technika při vytváření matematického modelu, počítačové simulace nějakého komplexního systému.

Řešení soustav lineárních rovnic se uplatňuje ve speciálních optimalizačních úlohách nazývaných lineární programování.

Velmi často jsou koeficienty rovnic i hledaná řešení reálná nebo komplexní čísla, ale celá teorie lineární algebry i její algoritmy platí, i když se namísto čísel vezmou prvky libovolného algebraického tělesa. Pro řešení soustav v jiných algebraických strukturách byly vybudovány jiné postupy a jiné teorie. Například pro okruh celých čísel poskytuje celočíselné lineární programování řadu metod pro nalezení „nejlepšího“ celočíselného řešení. Dalším příkladem je teorie Gröbnerových bází, v níž se pro koeficienty i neznámé používají polynomy. Ještě exotičtějším příkladem je tropická geometrie.

Základní ukázky

Triviální příklad

Soustava jedné rovnice o jedné reálné neznámé

${\displaystyle 2x=4}$

má jednoznačné řešení

${\displaystyle x=2.}$

Nicméně, za soustavu bývá zpravidla považován systém s alespoň dvěma rovnicemi.

Jednoduchý netriviální příklad

Nejjednodušší netriviální soustavu lineárních rovnic tvoří dvě rovnice o dvou neznámých, například:

${\displaystyle {\begin{array}{rcrcr}2x&+&3y&=&6\\4x&+&9y&=&15\end{array}}}$

Tuto soustavu lze vyřešit tak, že se z první rovnice vyjádří ${\displaystyle x}$ v závislosti na ${\displaystyle y}$:

${\displaystyle x=3-{\frac {3}{2}}y}$

a tento výraz se dosadí do druhé rovnice:

${\displaystyle 4\left(3-{\frac {3}{2}}y\right)+9y=15.}$

Výsledná rovnice má pouze jednu neznámou ${\displaystyle y}$ s řešením ${\displaystyle y=1}$. Zpětným dosazením do první rovnice lze dopočítat hodnotu neznámé ${\displaystyle x={\frac {3}{2}}}$.

Uvedený postup lze zobecnit pro soustavy s více neznámými (viz odstavec „eliminace neznámých“ níže nebo článek o elementární algebře).

Obecný tvar

Soustava ${\displaystyle m}$ lineárních rovnic o ${\displaystyle n}$ neznámých ^[1] bývá obvykle zapsána ve tvaru

${\displaystyle {\begin{array}{rcr}a_{11}x_{1}+a_{12}x_{2}+\dots +a_{1n}x_{n}&=&b_{1}\\a_{21}x_{1}+a_{22}x_{2}+\dots +a_{2n}x_{n}&=&b_{2}\\&\vdots &\\a_{m1}x_{1}+a_{m2}x_{2}+\dots +a_{mn}x_{n}&=&b_{m}\\\end{array}}}$

kde proměnné ${\displaystyle x_{1}}$, … ,${\displaystyle x_{n}}$ jsou neznámé a čísla ${\displaystyle a_{ij}}$ jsou koeficienty soustavy. Čísla ${\displaystyle b_{i}}$, kde ${\displaystyle i=1,2,...,m}$, jsou absolutní členy soustavy (též tzv. pravá strana soustavy). Koeficienty i absolutní členy mohou být prvky libovolného tělesa, tedy kromě reálných čísel jimi mohou být např. i komplexní čísla.

Soustavu lze popsat i úsporněji, např. ve složkovém zápisu:

${\displaystyle \sum _{j=1}^{n}a_{ij}x_{j}=b_{i}}$ pro ${\displaystyle i=1,2,...,m}$.

Maticová rovnice

Koeficienty soustavy bývají obvykle uspořádány do matice:

${\displaystyle {\boldsymbol {A}}={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{pmatrix}}}$

Tuto matici nazýváme matice soustavy.

Pro neznámé a pravou stranu soustavy se použijí sloupcové vektory

${\displaystyle {\boldsymbol {x}}={\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{pmatrix}}}$

${\displaystyle {\boldsymbol {b}}={\begin{pmatrix}b_{1}\\b_{2}\\\vdots \\b_{m}\end{pmatrix}}}$

Celou soustavu rovnic je pak lze zapsat s pomocí maticového součinu jedinou rovnicí

${\displaystyle {\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{pmatrix}}{\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{pmatrix}}={\begin{pmatrix}b_{1}\\b_{2}\\\vdots \\b_{m}\end{pmatrix}}}$

neboli

${\displaystyle {\boldsymbol {A}}{\boldsymbol {x}}={\boldsymbol {b}}}$

Pro výpočet řešení soustavy lineárních rovnic bývá často využívána tzv. rozšířená matice soustavy

${\displaystyle ({\boldsymbol {A}}|{\boldsymbol {b}})=\left({\begin{array}{cccc|c}a_{11}&a_{12}&\cdots &a_{1n}&b_{1}\\a_{21}&a_{22}&\cdots &a_{2n}&b_{2}\\\vdots &\vdots &\ddots &\vdots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}&b_{m}\end{array}}\right)}$

ze které lze zjistit existenci a jednoznačnost řešení, např. Gaussovou eliminační metodou.

Vektorová rovnice

Na řešení soustavy lineárních rovnic lze pohlížet i tak, že neznámé jsou koeficienty lineární kombinace, v níž je vektor pravých stran zapsán pomocí sloupcových vektorů koeficientů:

${\displaystyle x_{1}{\begin{pmatrix}a_{11}\\a_{21}\\\vdots \\a_{m1}\end{pmatrix}}+x_{2}{\begin{pmatrix}a_{12}\\a_{22}\\\vdots \\a_{m2}\end{pmatrix}}+\dots +x_{n}{\begin{pmatrix}a_{1n}\\a_{2n}\\\vdots \\a_{mn}\end{pmatrix}}={\begin{pmatrix}b_{1}\\b_{2}\\\vdots \\b_{m}\end{pmatrix}}}$

Tento pohled umožňuje uplatnit veškeré nástroje z teorie vektorových prostorů (obecněji modulů). Například množina všech možných lineárních kombinací vektorů na levé straně se nazývá lineární obal a uvedená rovnice má řešení, právě když se vektor pravých stran patří do tohoto obalu.

Homogenní soustava lineárních rovnic

Jsou-li všechny absolutní členy soustavy rovny nule, nazývá se soustava homogenní. Homogenní soustavy mají zápis ve tvaru

${\displaystyle {\boldsymbol {A}}{\boldsymbol {x}}={\boldsymbol {0}}}$,

což v rozvinutém tvaru znamená

${\displaystyle {\begin{array}{rcrcrcr}a_{11}x_{1}&+&a_{12}x_{2}&+\cdots +&a_{1n}x_{n}&=&0\\a_{21}x_{1}&+&a_{22}x_{2}&+\cdots +&a_{2n}x_{n}&=&0\\&&&&&\vdots \;\ &&\\a_{m1}x_{1}&+&a_{m2}x_{2}&+\cdots +&a_{mn}x_{n}&=&0\\\end{array}}}$

neboli

${\displaystyle \sum _{j=1}^{n}a_{ij}x_{j}=0}$ pro ${\displaystyle i=1,2,...,m}$,

Pokud je alespoň jeden z absolutních členů ${\displaystyle b_{i}}$ nenulový, jde o nehomogenní soustavu lineárních rovnic.

Každá homogenní soustava má alespoň jedno řešení, označované jako nulové (neboli triviální) řešení, ve kterém je každé neznámé přiřazeno číslo 0. Pokud je matice soustavy regulární, jde o jediné řešení. Je-li naopak singulární, je řešení více.

Množina řešení homogenní soustavy lineárních rovnic ${\displaystyle {\boldsymbol {A}}{\boldsymbol {x}}={\boldsymbol {0}}}$ má následující vlastnosti:

• Jsou-li ${\displaystyle {\boldsymbol {u}}}$ a ${\displaystyle {\boldsymbol {v}}}$ jsou dvě řešení, pak jejich vektorový součet ${\displaystyle {\boldsymbol {u}}+{\boldsymbol {v}}}$ je také řešením.
• Je-li ${\displaystyle {\boldsymbol {u}}}$ řešení soustavy a ${\displaystyle r}$ je libovolný skalár, pak ${\displaystyle r{\boldsymbol {u}}}$ je také řešením.

Jinými slovy, množina řešení tvoří vektorový prostor nazývaný jádro matice ${\displaystyle {\boldsymbol {A}}}$. Jádro se značí ${\displaystyle \ker {\boldsymbol {A}}}$ (z anglického kernel = jádro). Někdy se též nazývá nulový prostor matice ${\displaystyle {\boldsymbol {A}}}$.

Množina řešení

Při řešení nehomogenní soustavy nad nekonečným tělesem, což jsou například reálná či komplexní čísla, mohou nastat následující případy:

• soustava nemá řešení
• soustava má jedno řešení
• soustava má nekonečně mnoho řešení

Nad konečnými tělesy soustava nemá žádné řešení nebo jich může mít jen konečně mnoho (jedno nebo více).

Homogenní soustava lineárních algebraických rovnic má vždy triviální řešení, tzn. ${\displaystyle x_{i}=0}$ pro všechna ${\displaystyle i}$.

Geometrická interpretace

Množiny řešení soustav o dvou reálných neznámých lze znázornit v euklidovské rovině v níž osy odpovídají neznámým ${\displaystyle x}$ a ${\displaystyle y}$. Lineární rovnice odpovídají přímkám (s výjimkou triviálních rovnic se všemi koeficienty nulovými). Protože řešení soustavy musí splňovat všechny rovnice, tvoří množina řešení průnik těchto přímek. Průnikem pak může být buď jediný bod, prázdná množina nebo i přímka - to v případě, že přímky odpovídající rovnicím splývají.

Lineární rovnice o třech reálných neznámých určuje zpravidla rovinu v trojrozměrném euklidovském prostoru. Množina řešení je pak průsečíkem těchto rovin a může to být buď rovina, přímka, jeden bod nebo prázdná množina. Například rovnoběžné roviny v prostoru se neprotínají vůbec.

Je-li neznámých ${\displaystyle n}$, pak netriviální lineární rovnice určují nadroviny v ${\displaystyle n}$-rozměrném prostoru. Množina řešení je průnikem těchto nadrovin a má dimenzi nejvýše ${\displaystyle n-1}$ (vyjma triviálního případu, kdy matice soustavy je nulová).

Případy v obecné poloze

Podle počtu rovnic a neznámých se rozlišují následující případy:

• Má-li soustava stejný počet rovnic jako neznámých, bývá její řešení často jednoznačné.
• Má-li soustava více rovnic než neznámých, nazývá se přeurčená. U soustav s daty z praxe zpravidla nemívá řešení.
• Má-li soustava méně rovnic než neznámých, nazývá se nedourčená. Řešení je zpravidla více. Soustava nemusí mít řešení, ale řešení nikdy není jednoznačné.

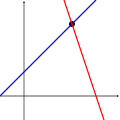
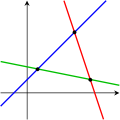
Následující obrázky ilustrují tuto trichotomii v případě dvou neznámých:

Jedna rovnice	Dvě rovnice	Tři rovnice

První soustava má nekonečně mnoho řešení, jmenovitě všechny body na modré přímce. Druhá soustava má jediné řešení, a to průnik dvou přímek. Ve třetím případě soustava nemá žádné řešení, protože tři zakreslené přímky nemají společný průnik.

Je třeba mít na paměti, že obrázky výše ukazují pouze obvyklý případ, kdy jsou přímky v tzv. obecné poloze. Může se stát, že soustava dvou rovnic o dvou neznámých nemá řešení a to tehdy, jsou-li přímky rovnoběžné. Podobně se u soustavy tří rovnic mohou odpovídající tři přímky protnout ve společném bodě anebo mohou některé přímky splynout.

Formálně řečeno, soustava lineárních rovnic se chová odlišně od uvedených případů v obecné poloze, pokud jsou rovnice lineárně závislé, nebo pokud je soustava nekonzistentní a nemá více rovnic než neznámých.

Vlastnosti

Nezávislost

Stane-li se, že některá rovnice soustavy je lineární kombinací ostatních rovnic, pak tato rovnice neklade na řešení soustavy žádné další podmínky, je nadbytečná (nadpočetná), a lze ji ze soustavy rovnic vyloučit aniž by se změnila množina řešení. Tento postup lze opakovat, dokud výsledná soustava rovnic neobsahuje jen lineárně nezávislé rovnice.

Rovnice lineární soustavy jsou nezávislé, pokud žádnou z nich nelze algebraicky odvodit z ostatních.

Například rovnice

${\displaystyle 3x+2y=6}$ a ${\displaystyle 6x+4y=12}$

jsou závislé — jde o stejné rovnice, jen ve druhé jsou všechny koeficienty dvojnásobné. Obě odpovídají téže přímce.

Rovnice soustavy

${\displaystyle {\begin{array}{rcrcr}x&-&2y&=&-1\\3x&+&5y&=&8\\4x&+&3y&=&7\end{array}}}$

jsou také závislé, protože třetí rovnice je součtem předchozích dvou. Ve skutečnosti lze kteroukoli z těchto rovnic odvodit z ostatních dvou a kteroukoli z rovnic lze odstranit, aniž by se změnila množina řešení. Odpovídající tři přímky se protínají v jednom bodě.

Konzistence

Lineárně nezávislé rovnice mohou být vzájemně rozporné, tzn. levou stranu některé z rovnic lze vyjádřit jako lineární kombinaci levých stran ostatních, avšak pravá strana této rovnice není stejnou lineární kombinací pravých stran. Soustavu pak lze upravit ekvivalentními úpravami tak, že bude obsahovat dvě rovnice, jejichž levé strany jsou shodné, avšak pravé strany budou rozdílné. Výsledná soustava je vnitřně rozporná, neboli nekonzistentní a nemá žádné řešení.

V ostatních případech je soustava konzistentní, což platí speciálně pro soustavy, jejichž levé strany jsou lineárně nezávislé.

U nekonzistentních soustav je možné z rovnic odvodit spor, třeba jako výrok ${\displaystyle 0=1}$.

Například rovnice

${\displaystyle 3x+2y=6}$ a ${\displaystyle 3x+2y=12}$

jsou nekonzistentní. Spor ${\displaystyle 0=1}$ lze získat vydělením jejich rozdílu šesti. Odpovídající přímky jsou rovnoběžné.

Soustava

${\displaystyle {\begin{array}{rcrcr}x&+&y&=&1\\2x&+&y&=&1\\3x&+&2y&=&3\end{array}}}$

je nekonzistentní, protože součet prvních dvou je ${\displaystyle 3x+2y=2}$, a následné odečtení třetí dá ${\displaystyle 0=1}$. Na druhou stranu, jakákoli dvojice z těchto tří rovnic tvoří konzistentní soustavu, čili má řešení. Stejná situace může nastat pro více rovnic a proměnných.

Frobeniova věta

Nehomogenní soustava lineárních algebraických rovnic má řešení, právě když hodnost matice soustavy je rovna hodnosti rozšířené matice soustavy: ${\displaystyle \operatorname {rank} ({\boldsymbol {A}}|{\boldsymbol {b}})=\operatorname {rank} {\boldsymbol {A}}}$. V tomto případě je soustava konzistentní. Pokud je hodnost matice ${\displaystyle {\boldsymbol {A}}}$ rovna počtu neznámých, má soustava jedno řešení; pokud je ${\displaystyle \operatorname {rank} {\boldsymbol {A}}}$ menší než počet neznámých, je řešení více.

Hodnost matice ${\displaystyle {\boldsymbol {A}}}$ nemůže být z definice větší než počet neznámých, ale je-li hodnost rozšířené matice soustavy ${\displaystyle ({\boldsymbol {A}}|{\boldsymbol {b}})}$ větší než počet neznámých, nemůže být splněna podmínka Frobeniovy věty, soustava je tudíž nekonzistentní a nemá žádné řešení.

Ekvivalence soustav

Pokud dvě soustavy lineárních rovnic používají stejnou množinu neznámých a přitom lze každou z rovnic druhé soustavy odvodit algebraicky z rovnic v první i naopak, říká se o soustavách, že jsou si navzájem ekvivalentní. Nekonzistentní páry soustav jsou si vždy ekvivalentní. U konzistentních ekvivalentních soustav platí, že každá rovnice jedné z nich je lineární kombinací rovnic druhé. Dvě soustavy jsou si tudíž ekvivalentní, právě když mají stejnou množinu řešení.

Množiny řešení homogenních a nehomogenních soustav

Je-li ${\displaystyle {\boldsymbol {p}}}$ nějaké konkrétní řešení soustavy ${\displaystyle {\boldsymbol {Ax}}={\boldsymbol {b}}}$, pak lze celou množinu řešení této soustavy popsat výrazem ${\displaystyle \{{\boldsymbol {p}}+{\boldsymbol {v}}\colon {\boldsymbol {v}}\in \ker {\boldsymbol {A}}\}}$. Zde ${\displaystyle \ker {\boldsymbol {A}}}$ značí jádro matice a tvoří ho všechna řešení soustavy ${\displaystyle {\boldsymbol {Ax}}={\boldsymbol {0}}}$.

Jinými slovy, množinu řešení soustavy ${\displaystyle {\boldsymbol {Ax}}={\boldsymbol {b}}}$ lze získat posunem jádra matice ${\displaystyle {\boldsymbol {A}}}$ o vektor ${\displaystyle {\boldsymbol {p}}}$.

Metody řešení

Popis řešení

Má-li soustava jednoznačné řešení, lze ji přepsat na systém rovnic, v nichž na levé straně je vždy jen jedna neznámá a na pravé straně její hodnota, např. ${\displaystyle x=3}$, ${\displaystyle y=-2}$ a ${\displaystyle z=6}$. Je-li dáno nějaké pořadí neznámých, například abecední, může být řešení popsáno vektorem hodnot, jako je ${\displaystyle (3,-2,6)^{\mathsf {T}}}$ v uvedeném příkladě.

Aby bylo možné popsat i nekonečné množiny řešení, jsou některé neznámé označeny jako volné proměnné (nebo nezávislé nebo jako parametry), což znamená, že mohou nabývat libovolných hodnot. Zbývající proměnné jsou pak závislé na hodnotách volných proměnných. Někdy se nazývají bázické proměnné.

Řešení reálné soustavy

${\displaystyle {\begin{array}{rcrcr}x&+&3y&-&2z&=&5\\3x&+&5y&+&6z&=&7\end{array}}}$

lze popsat rovnicemi:

${\displaystyle x=-7z-1}$ a ${\displaystyle y=3z+2{\text{.}}}$

Zde ${\displaystyle z}$ je volná proměnná, zatímco ${\displaystyle x}$ a ${\displaystyle y}$ závisí na ${\displaystyle z}$. Jakékoli řešení lze získat tak, že se nejprve zvolí hodnota ${\displaystyle z}$ a z ní se spočítají odpovídající hodnoty pro ${\displaystyle x}$ a ${\displaystyle y}$.

Každá volná proměnná dává prostoru řešení jeden stupeň volnosti. Počet volných proměnných je dimenze množiny řešení. Například řešení výše uvedené soustavy tvoří jednodimenzionální prostor - přímku, protože každé řešení lze získat volbou hodnoty jednoho parametru ${\displaystyle z}$.

Různé volby volné proměnné poskytují různé popisy stejné množiny řešení. Například

${\displaystyle y=-{\frac {3}{7}}x+{\frac {11}{7}}}$ a ${\displaystyle z=-{\frac {1}{7}}x-{\frac {1}{7}}}$.

je alternativním popisem téže množiny řešení, jen ${\displaystyle x}$ je zde volná proměnná a ${\displaystyle y}$ a ${\displaystyle z}$ jsou závislé.

Eliminace proměnných

Nejjednodušší metodou řešení soustav lineárních rovnic je eliminace proměnných. Tuto metodu lze popsat následovně:

1. Z první rovnice se vyjádří jedna z neznámých pomocí ostatních.
2. Tento výraz se dosadí do zbývajících rovnic, čím se získá soustava rovnic, která má o jednu rovnici a o jednu neznámou méně.
3. Kroky 1 a 2 se opakují tak dlouho, dokud se soustava nezredukuje na jedinou lineární rovnici.
4. Výsledná rovnice se vyřeší a pak zpětným dosazením se určí celé řešení.

Například v následující soustavě:

${\displaystyle {\begin{array}{rcrcrcr}x&+&3y&-&2z&=&5\\3x&+&5y&+&6z&=&7\\2x&+&4y&+&3z&=&8\end{array}}}$

lze z první rovnice vyjádřit ${\displaystyle x=5+2z-3y}$. Jeho dosazením do druhé a třetí rovnice

${\displaystyle {\begin{array}{rcrcrcr}3(5+2z-3y)&+&5y&+&6z&=&7\\2(5+2z-3y)&+&4y&+&3z&=&8\end{array}}}$

se soustava zredukuje na

${\displaystyle {\begin{array}{rcrcr}-y&+&3z&=&-2\\-2y&+&7z&=&-2\end{array}}}$

Z první rovnice lze vyjádřit ${\displaystyle y=3z+2}$ a jeho dosazením do druhé získat

${\displaystyle {\begin{array}{rcl}-2(3z+2)+7z&=&-2\\\Rightarrow z&=&2\end{array}}}$

Dosazení ${\displaystyle z=2}$ do vyjádření pro ${\displaystyle y}$ dává ${\displaystyle y=8}$. Z hodnot ${\displaystyle y}$ a ${\displaystyle z}$ se pak dopočítá ${\displaystyle x=-15}$. Řešením soustavy je uspořádaná trojice ${\displaystyle (x,y,z)=(-15,8,2)}$.

Gaussova eliminace

Gaussova eliminace vychází z poznatku, že rozšířenou matici soustavy lze měnit vhodným způsobem tak, aniž by se změnila množina řešení soustavy. Pro tento účel se používají následující elementární ekvivalentní řádkové úpravy:

Typ 1 : změna pořadí řádků

Typ 2 : vynásobení řádku nenulovým skalárem

Typ 3 : přičtení jednoho řádku (nebo jeho skalárního násobku) k jinému

Uvedené operace jsou vratné, a proto získaná rozšířená matice odpovídá soustavě, která je ekvivalentní původní.

Redukci lze provádět různými způsoby. Mezi jednoduché patří Gaussova eliminace a Gaussova–Jordanova eliminace. Gaussova–Jordanova eliminace matice soustavy z předchozího příkladu odpovídá následujícímu výpočtu:

${\displaystyle {\begin{aligned}\left({\begin{array}{rrr|r}1&3&-2&5\\3&5&6&7\\2&4&3&8\end{array}}\right)&\sim \left({\begin{array}{rrr|r}1&3&-2&5\\0&-4&12&-8\\2&4&3&8\end{array}}\right)\sim \left({\begin{array}{rrr|r}1&3&-2&5\\0&-4&12&-8\\0&-2&7&-2\end{array}}\right)\sim \left({\begin{array}{rrr|r}1&3&-2&5\\0&1&-3&2\\0&-2&7&-2\end{array}}\right)\\&\sim \left({\begin{array}{rrr|r}1&3&-2&5\\0&1&-3&2\\0&0&1&2\end{array}}\right)\sim \left({\begin{array}{rrr|r}1&3&-2&5\\0&1&0&8\\0&0&1&2\end{array}}\right)\sim \left({\begin{array}{rrr|r}1&3&0&9\\0&1&0&8\\0&0&1&2\end{array}}\right)\sim \left({\begin{array}{rrr|r}1&0&0&-15\\0&1&0&8\\0&0&1&2\end{array}}\right).\end{aligned}}}$

Z poslední matice lze snadno odvodit řešení ${\displaystyle x=-15}$, ${\displaystyle y=8}$ a ${\displaystyle z=2}$. Srovnání s výpočtem v předchozím odstavci o eliminaci proměnných naznačuje, že obě metody jsou ve skutečnosti stejné; rozdíl je jen v zápisu výpočtu.

Cramerovo pravidlo

Cramerovo pravidlo poskytuje vzorec pro řešení soustav lineárních rovnic s regulární maticí. Hodnoty neznámých jsou dány podílem dvou determinantů. Například řešení soustavy

${\displaystyle {\begin{array}{rcrcr}x&+&3y&-&2z&=&5\\3x&+&5y&+&6z&=&7\\2x&+&4y&+&3z&=&8\end{array}}}$

je dáno podíly

${\displaystyle x={\frac {\,{\begin{vmatrix}5&3&-2\\7&5&6\\8&4&3\end{vmatrix}}\,}{\,{\begin{vmatrix}1&3&-2\\3&5&6\\2&4&3\end{vmatrix}}\,}},\;\;\;\;y={\frac {\,{\begin{vmatrix}1&5&-2\\3&7&6\\2&8&3\end{vmatrix}}\,}{\,{\begin{vmatrix}1&3&-2\\3&5&6\\2&4&3\end{vmatrix}}\,}},\;\;\;\;z={\frac {\,{\begin{vmatrix}1&3&5\\3&5&7\\2&4&8\end{vmatrix}}\,}{\,{\begin{vmatrix}1&3&-2\\3&5&6\\2&4&3\end{vmatrix}}\,}}.}$

Pro každou proměnnou je ve jmenovateli determinant matice koeficientů soustavy, zatímco v čitateli je determinant obdobné matice, jen sloupec odpovídající neznámé byl nahrazen vektorem pravých stran.

Cramerovo pravidlo je důležité spíše z teoretického hlediska, protože výpočet mnoha velkých determinantů je poněkud těžkopádný. (Velké determinanty se skutečně nejsnáze vypočítají pomocí redukce řádků.) Navíc je Cramerovo pravidlo numericky nestabilní, takže není vhodné ani pro přesné řešení malých soustav, ledaže by aritmetické operace byly prováděny v racionální aritmetice s neomezenou přesností. 

Maticové řešení

Množinu řešení soustav ${\displaystyle {\boldsymbol {A}}{\boldsymbol {x}}={\boldsymbol {b}}}$ lze popsat i maticovým výrazem. U soustav s regulární maticí ${\displaystyle {\boldsymbol {A}}}$ je jednoznačné řešení dané vztahem

${\displaystyle {\boldsymbol {x}}={\boldsymbol {A}}^{-1}{\boldsymbol {b}}}$

kde ${\displaystyle {\boldsymbol {A}}^{-1}}$ je inverzní matice k matici ${\displaystyle {\boldsymbol {A}}}$.

V obecném případě, tedy bez ohledu na to, zda je matice soustavy regulární ba dokonce čtvercová, lze všechna řešení (pokud nějaká existují) popsat pomocí Mooreovy–Penroseovy inverze k ${\displaystyle {\boldsymbol {A}}}$, označované ${\displaystyle {\boldsymbol {A}}^{+}}$ následovně:

${\displaystyle {\boldsymbol {x}}={\boldsymbol {A}}^{+}{\boldsymbol {b}}+\left(\mathbf {I} -{\boldsymbol {A}}^{+}{\boldsymbol {A}}\right){\boldsymbol {w}}}$

kde ${\displaystyle {\boldsymbol {w}}}$ je vektor volných parametrů. Nezbytnou a postačující podmínkou pro existenci řešení je, že potenciální řešení získané dosazením ${\displaystyle {\boldsymbol {w}}={\boldsymbol {0}}}$ splňuje ${\displaystyle {\boldsymbol {A}}{\boldsymbol {x}}={\boldsymbol {b}}}$, neboli ${\displaystyle {\boldsymbol {A}}{\boldsymbol {A}}^{+}{\boldsymbol {b}}={\boldsymbol {b}}.}$ Pokud tato podmínka neplatí, soustava rovnic je nekonzistentní a nemá žádné řešení. Pokud podmínka platí, soustava je konzistentní a má alespoň jedno řešení. Například ve výše uvedeném případě, kdy ${\displaystyle {\boldsymbol {A}}}$ je čtvercová a má plnou hodnost, se ${\displaystyle {\boldsymbol {A}}^{+}}$ shoduje s ${\displaystyle {\boldsymbol {A}}^{-1}}$ a obecná rovnice řešení se zjednoduší na již známý vztah

${\displaystyle {\boldsymbol {x}}={\boldsymbol {A}}^{-1}{\boldsymbol {b}}+\left(\mathbf {I} -{\boldsymbol {A}}^{-1}{\boldsymbol {A}}\right){\boldsymbol {w}}={\boldsymbol {A}}^{-1}{\boldsymbol {b}}+\left(\mathbf {I} -\mathbf {I} \right){\boldsymbol {w}}={\boldsymbol {A}}^{-1}{\boldsymbol {b}}}$

Během algebraických úprav byl vektor ${\displaystyle {\boldsymbol {w}}}$ zcela eliminován a řešení je jednoznačné. V ostatních případech však ${\displaystyle {\boldsymbol {w}}}$ zůstane, přičemž volby vektoru ${\displaystyle {\boldsymbol {w}}}$ určují množinu řešení rovnice.

Jiné metody

Zatímco soustavy tří nebo čtyř rovnic lze snadno vyřešit ručně, pro větší soustavy se často používají počítače. Standardní algoritmus pro řešení soustav lineárních rovnic bývá založen na Gaussově eliminaci. Pro numerickou stabilitu je vhodné se vyvarovat dělení malými čísly, například volbou pořadí rovnic. Tento proces se nazývá pivotování. Namísto Gaussovy eliminace, se spíše počítá související LU rozklad matice ${\displaystyle {\boldsymbol {A}}}$. Ten bývá výhodný, zejména je-li třeba vyřešit několik soustav se shodnou maticí ${\displaystyle {\boldsymbol {A}}}$, ale různými vektory ${\displaystyle {\boldsymbol {b}}}$.

Rychlejší anebo přesnější algoritmy byly navrženy pro matice ${\displaystyle {\boldsymbol {A}}}$ s nějakou speciální strukturou. Například Choleského rozklad bývá rychlejší pro soustavy s pozitivně definitní maticí. Levinsonova rekurze je rychlá metoda pro Toeplitzovy matice. Dalším příkladem matic, pro něž jsou známy speciální metody jsou řídké matice, což jsou matice s mnoha nulovými prvky. Tyto matice se hojně objevují v praktických aplikacích.

Numerická řešení homogenní soustavy lze nalézt pomocí singulárního rozkladu matice.

Zcela jiný přístup bývá třeba u velmi velkých soustav, jejichž přesné řešení by si vyžádalo příliš mnoho času nebo paměti. Pro ně se používají přibližné iterační metody. Po nalezení počáteční aproximace řešení (která nemusí být vůbec přesná) je přibližné řešení postupně zpřesňováno, dokud se dostatečně nepřiblíží ke skutečnému řešení. Efektivitu iteračních metod může být u některých řídkých matic zvýšena pomocí náhodnosti. ^[2]

Pro soustavy lineárních rovnic byl navržen i kvantový algoritmus. ^[3]

Odkazy

Reference

V tomto článku byl použit překlad textu z článku System of linear equations na anglické Wikipedii.

Literatura

• BEČVÁŘ, Jindřich. Lineární algebra. 1.. vyd. Praha: Matfyzpress, 2019. 436 s. ISBN 978-80-7378-392-1. 
• HLADÍK, Milan. Lineární algebra (nejen) pro informatiky. 1.. vyd. Praha: Matfyzpress, 2019. 328 s. ISBN 978-80-7378-378-5. 
• OLŠÁK, Petr. Lineární algebra [online]. Praha: 2007 [cit. 2023-02-20]. Dostupné online. 
• MOTL, Luboš; ZAHRADNÍK, Miloš. Pěstujeme lineární algebru [online]. [cit. 2023-02-20]. Dostupné online. 

Související články

• Hodnost matice
• Inverzní matice
• Gaussova eliminační metoda
• Cramerovo pravidlo
• LU rozklad
• Choleského rozklad
• Jacobiho metoda
• Metoda nejmenších čtverců
• Soustava rovnic
• Rovnice

Externí odkazy

• Obrázky, zvuky či videa k tématu soustava lineárních rovnic na Wikimedia Commons
• Online výpočet soustav lineárních rovnic