Souvislá množina

Souvislá množina je v topologii množina, kterou nelze rozdělit na dvě disjunktní, neprázdné a otevřené podmnožiny.
Definice
Souvislá množina
Množina , topologického či metrického prostoru se nazývá souvislá, pokud kdykoli , jsou množiny otevřené v M takové, že
- a
- .
Pak buď nebo
Ekvivalentní definice
- Množina , topologického či metrického prostoru se nazývá souvislá, pokud kdykoli , jsou množiny uzavřené v M takové, že
- a
- .
Pak buď nebo
- Je-li spojité zobrazení a , pak .
Souvislý prostor
Topologický prostor je souvislý, je-li svou vlastní souvislou podmnožinou.
Topologický prostor je souvislý právě tehdy, když jediné podmnožiny v , které jsou současně otevřené i uzavřené, jsou a . V opačném případě bývá prostor označován jako nesouvislý.
Komponenta souvislosti
Komponenta souvislosti množiny je každá její maximální (vzhledem k ) souvislá podmnožina.
Odkazy
Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu souvislá množina na Wikimedia Commons
Obrázky, zvuky či videa k tématu souvislá množina na Wikimedia Commons
Média použitá na této stránce
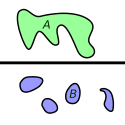
The space A at top is a connected space. The space B at bottom is disconnected. Created in Inkscape by Caesura for Connected space.