Statika

Statika je částí mechaniky, která se zabývá hmotnými tělesy nacházejícími se v relativním klidu k určité vztažné soustavě, dále silami, které mezi takovýmito tělesy působí a rovnováhou celého systému. Dynamika, na rozdíl od statiky, bere do úvahy navíc také pohyb hmotného tělesa, tedy působení setrvačných a tlumících sil. Kinematika je součástí dynamiky, ale studuje pohyb těles pouze z geometrického a časového hlediska, bez zkoumání jeho příčin.[1] Statiku lze rozlišit na teoretickou a aplikovanou.
Historie

Nauka o rovnováze, neboli statika, sahá daleko do starověku. Potřeba této nauky vyvstala používáním pomůcek pro zvládání těžké fyzické práce, např. páky, šroubu, kladkostroje a nakloněné roviny. Teoretický princip páky popsal v Řecku ve 3. stol. př. n. l. Archimédés a položil tím i základ pro pozdější hojné využívání např. klínu, nakloněné roviny a otočné lanové kladky. Praktické příklady využívání principů ulehčujících člověku každodenní život byly přesto prokazatelně doloženy již z doby daleko dřívější, např. kolem roku 1550 př. n. l. – tzv. šadúf (pozdější arabské pojmenování), což je pákové zařízení na přečerpávání vody do zavlažovacích stružek na polích.[2] Použití kladkostroje je doloženo v Řecku již z doby kolem roku 700 př. n. l.[3] Archimédovi přísluší také velký přínos v oblasti hydrostatiky, o který se zasloužil formulováním hydrostatického zákona. Tento známý princip, jehož objev byl údajně doprovozen zvoláním Heuréka! (Nalezl jsem!), říká, že těleso ponořené do kapaliny je nadlehčováno silou odpovídající tíze vody tělesem vytlačené.[4] Pojmy těžiště nebo specifická váha se poprvé doložitelně objevují také ve starém Řecku. O rozsáhlé praktické využití těchto teoretických prací se ale zasloužili až Římané, nikoli Řekové, podařilo se jim je totiž technicky provést.[4] Tato prvotní statika vrcholí větou o virtuálních posunech: Vytvoříme-li součin každé síly s dráhou, kterou její působiště urazilo ve směru síly, pokud takový pohyb nastal, a provedeme-li součet všech těchto součinů (při zachování znamének odpovídajících orientaci sil), pak rovnováha nastává, pokud tento součet dává nulu. K formulaci tohoto poznatku v roce 1600 bylo zapotřebí několik tisíciletí značného úsilí. Posledním v řadě těch, kteří se zasloužili o jeho řešení, byl holandský matematik Simon Stevin, známý jako Simon z Brugg[5] (1548–1620). Ten s geniální intuicí prozkoumal rovnováhu na nakloněné rovině a přitom odhalil možnost rozkladu síly na její složky a zavedl pojem silový rovnoběžník.[5][6]
Teoretická statika
Teoretická statika zkoumá všeobecně platné zákony relativního klidu bez ohledu na možnosti praktického využití.[1] Statiku lze obecně dělit podle skupenství zkoumaných objektů na statiku pevných těles, statiku kapalin (hydrostatiku) a statiku plynů (aerostatiku). Statika pracuje se základními pojmy jako jsou prostor, síla, moment, vektor, rovnováha, stabilita, moment setrvačnosti, soustava sil a další.
Základní pojmy
Prostor. Statika je jako součást klasické fyziky uvažována v eukleidovském prostoru. Takový prostor je definován pomocí Eukleidových definicí a axiomů, které Eukleides publikoval v díle Základy (řecky Stoicheia) již v době kolem 300 př. n. l.. Eukleidovský prostor je popisem prostoru jak ho vnímá člověk v běžném životě. Prostor je, mimo jiné, definován počtem dimenzí. Prostor dimenze 1 je představován pomocí jednorozměrné křivky, např. přímky, prostor dimenze 2 má o jeden (kolmý) rozměr víc a je reprezentován rovinou. Pokud přidáme další rozměr, dostáváme se do prostoru o 3 dimenzích. Analogicky lze přidávat další dimenze, které obecně nemusejí být pouze délkové. Za 4-dimenzionální prostor je označován prostoročas, kde další dimenzi představuje čas. Za prostor dimenze 0 (nula) je označován bod. Problémy statiky lze popisovat v prostorech různých dimenzí.
Síla je vektorová fyzikální veličina, vyjadřující míru vzájemného působení těles a polí. Síly se projevují statickými nebo dynamickými účinky na objekty. Statickým účinkem je deformace tělesa, která může být pružná, pokud platí Hookeův zákon, nebo plastická.
Moment síly je vektorová fyzikální veličina, která vyjadřuje míru otáčivého účinku síly. Tento účinek se vztahuje k danému momentovému bodu nebo přímce. Kolmá vzdálenost od osy síly k bodu se nazývá rameno síly. Pohybem síly ve směru svého působení se velikost momentu síly nemění. Vektor momentu síly je kolmý na rovinu síly a polohového vektoru působiště. Moment síly lze nahradit dvojicí sil, neboli soustavou dvou rovnoběžných sil stejně velkých, opačného smyslu a neležících v jednom paprsku.[7] Varignonova věta říká, že statický moment výslednice jakékoliv prostorové soustavy sil k libovolnému bodu v prostoru je roven vektorovému součtu statických momentů jednotlivých sil soustavy k témuž bodu.
Vektor představuje ve fyzice veličinu, mající kromě skalární, tedy číselné, velikosti i směr. Příkladem vektoru je síla, vždy má velikost a směr působení. Síly lze skládat podle zákona o skládání sil s využitím silového rovnoběžníku. Vektory se obvykle popisují pomocí souřadnic, přičemž záleží na počtu dimenzí prostoru a volbě souřadnicových os. Jsou definovány různé operace, které lze s vektory provádět, např. součet, součin, násobení vektoru číslem.
Rovnováha je jednou ze základních podmínek, které statika zkoumá. Podle počtu dimenzí prostoru, ve kterém je soustava sil vyšetřována, a vlastností působících sil (např. rovnoběžnost, společné působiště), jsou stanoveny odpovídající podmínky rovnováhy. Podmínka rovnováhy pro obecnou prostorovou soustavu sil zní: Obecná prostorová soustava sil působící na tuhé těleso je v rovnováze jen tehdy, když algebraické součty průmětů všech sil soustavy do každé ze tří navzájem kolmých (ještě obecněji i kosoúhlých) os x, y, z jsou rovny nule a když součty statických momentů všech sil soustavy k těmže osám jsou rovněž rovny nule.[8]
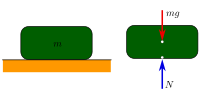
Zákony, principy a axiomy statiky
- zákon akce a reakce: Každá akce vyvolá reakci stejně velkou, ale opačného směru.
- princip superpozice účinků: možnost rozkládání a skládání sil a jejich účinků (platí pro lineární mechaniku)
- princip úměrnosti: poměrná změna akce (síly) vyvolává odpovídající poměrnou změnu reakce (platí pro lineární mechaniku)
- axiom 1: Vektor výslednice dvou sil působících na tuhé těleso v jednom bodu je tvořen úhlopříčkou rovnoběžníku o stranách rovných vektorům těchto sil.
- axiom 2: Dvě síly působící na tuhé těleso jsou v rovnováze tehdy, pokud jsou stejně velké, mají opačnou orientaci a působí na jedné přímce.
- axiom 3: K tělesu je možno přidat (resp. od něj odebrat) rovnovážnou soustavu sil, aniž by se tím změnil pohybový stav tuhého tělesa.[9]
Statika pevných těles
Statika pevných těles studuje pevná tělesa nacházející se v relativním klidu a síly, které na ně působí. Dělíme ji na statiku těles dokonale tuhých, pružných a plastických, s ohledem na povahu odezvy tělesa na působení sil, tzn. deformaci neboli přetvoření. U dokonale tuhého tělesa jde o idealizaci jeho deformačních vlastností, která ve skutečnosti nemůže nastat, ale její zavedení je výhodné pro zkoumání čistě pohybových účinků sil. Tato idealizace spočívá v uvažování nulových deformací tělesa při účinku libovolných sil zavedením jeho nekonečné tuhosti. Nekonečná tuhost má za následek šíření odezvy na působení síly maximální možnou rychlostí, tedy rychlostí světla. Idealizace dokonale tuhého tělesa je využívána při vyšetřování staticky určitých konstrukcí, kdy k určení vnitřních sil postačují pouze statické podmínky rovnováhy, bez uvažování podmínek deformačních. U skutečných těles je rychlost šíření odezvy v tělese vždy nižší než rychlost světla. Je to způsobeno postupnými změnami vzdáleností jednotlivých atomů látky, které těleso tvoří. Při působení osové tahové síly na volný konec prutu (např. zavěšením závaží na ukotvené ocelové lano) dojde k postupnému vzájemnému oddálení atomů v celé délce prutu až k bodu ukotvení, kde účinek síly vyrovná reakce. Délka prutu se vlivem nárůstu vzdáleností mezi atomy zvětší a prut zaujme nový tvar, odpovídající velikosti působící síly. Pokud se po odstranění zatěžující síly vrátí těleso zcela do původního tvaru, nazýváme tuto deformaci pružnou neboli elastickou. Pokud po odstranění síly zůstane těleso alespoň zčásti deformováno, jedná se o deformaci plastickou nebo pružnoplastickou. Výpočtem deformací a napětí konstrukcí za pružného i plastického stavu se zabývá teorie pružnosti a plasticity. S deformačními podmínkami rovnováhy je třeba uvažovat při vyšetřování staticky neurčitých konstrukcí, kde velikosti vnitřních sil závisejí i na přetvárných vlastnostech materiálů. Základním vztahem v teorii pružnosti pevných těles je hookeův zákon, vyjadřující závislost mezi působící silou a velikostí pružné deformace tělesa. Jednou z nejvýznamnějších aplikací statiky pevných těles je také Euler-Bernoulliova prutová teorie, která popisuje vztah mezi příčným zatížením a pootočením průřezu prutu.
Statika kapalin (hydrostatika)
Hydrostatika se zabývá studiem kapalin v relativním klidu. Pro zjednodušení se zavádí ideální kapalina, která má na rozdíl od reálné kapaliny ideální vlastnosti, a to nulovou stlačitelnost a nulové vnitřní tření. Aby byla kapalina v klidu, musejí být v rovnováze síly působící na každý její element. Pokud například uvažujeme jako element nekonečně malou krychličku, musejí být všechny síly působící na její strany v rovnováze, jinak dojde k pohybu krychličky ve směru převládající síly. Kapalina není schopná přenášet žádné smykové napětí (na rozdíl od pevné látky), ale lze působit normálovou tlakovou silou na plochu jejího povrchu. V kapalinách tedy neuvažujeme klasické síly v bodovém působišti, ale síly na ploše, neboli tlakové síly. Pokud vztáhneme tlakovou sílu na jednotkovou plochu, dostáváme fyzikální veličinu tlak. Tlak v kapalinách může být způsoben tím, že se kapalina nachází v silovém poli a každá její částice je tímto polem ovlivňována; pak hovoříme o vnitřním (hydrostatickém) tlaku v kapalinách. Pokud působí na plochu povrchu kapaliny vnější tlaková síla, například píst, hovoříme o tlaku vnějším.

V hydrostatice platí dva základní zákony, Archimédův zákon, který říká, že na těleso ponořené do kapaliny působí vztlaková síla odpovídající tíze kapaliny o stejném objemu jako je objem tělesa a Pascalův zákon říkající, že jestliže na kapalinu působí vnější tlaková síla, pak tlak v každém místě kapaliny vzroste o stejnou hodnotu..
Statika plynů (aerostatika)
Aerostatika se zabývá mechanickými vlastnostmi plynů a těles do nich ponořených. Plyny podobně jako kapaliny nejsou schopny díky své vnitřní struktuře přenášet smykové napětí a působí v nich obdoba hydrostatického tlaku – aerostatický tlak. Na rozdíl od kapalin je však jednou ze základních vlastností plynů objemová stlačitelnost. Pro zjednodušení se zavádí ideální plyn, který má na rozdíl od reálného plynu ideální vlastnosti, a to dokonalou stlačitelnost a nulové vnitřní tření. Vzhledem k podobnosti některých vlastností kapalin a plynů pro ně platí i obdobné zákonitosti. Do plynu lze například podobně jako do kapaliny ponořit těleso. Balón v atmosféře je nadnášen vztlakovou silou, kterou lze určit obdobou Archimédova zákona, známého především z hydrostatiky. Působením silového pole zemské gravitace na částice plynů atmosféry vzniká atmosférický tlak.
Aplikovaná statika
Aplikovaná statika řeší praktické technické problémy mnoha oborů lidské činnosti. Využívá k tomu poznatků a závěrů teoretické statiky, podpořených výsledky experimentálních výzkumů.[1] Největší uplatnění nalezla statika ve stavebním inženýrství a architektuře, vzhledem k tomu, že stavební konstrukce se nacházejí převážně v klidu a veškerá zatížení, která na ně působí, musejí být v rovnováze.

Statika stavebních konstrukcí
Obecně se označením statika stavebních konstrukcí rozumí celý soubor technických disciplín, využívaných při navrhování a posuzování stavebních konstrukcí. Jejím úkolem je optimální navržení konstrukce na účinky statických i dynamických zatížení.[1] Statika se v praxi zabývá vyšetřováním stavebních konstrukcí a jejich částí v různých prostorových úrovních a systémech. Účelem je stanovit takové dimenze jednotlivých prvků konstrukce, aby tato soustava přenesla požadovaná zatížení s předem definovanou bezpečností během předepsané životnosti konstrukce. Cílem je bezpečně přenést požadovaná působící zatížení pomocí nosných prvků konstrukce do základů. Ve statice se vychází z elementárních diferenciálních vztahů, ze kterých jsou odvozeny obecné algebraické vztahy mezi vnitřními silami a přetvořeními konstrukce. Tyto obecné prostorové vztahy jsou dále zjednodušovány na soustavy základních prvků, které jsou počítány a dimenzovány samostatně.
Statický výpočet
Statika stavebních konstrukcí se využívá při návrhu všech namáhaných, zejm. stavebních a strojních konstrukcí a jejich částí. Nejběžnějším výstupem je statický výpočet, resp. statický posudek, který je nezbytnou součástí stavebních projektových dokumentací v různých stupních, nejčastěji ve stupni pro stavební povolení či ohlášení stavby podle přílohy č. 1 k vyhlášce č. 499/2006 Sb. o dokumentaci staveb [1]. Statický posudek zpravidla zhotovuje a pro úřední účely vždy razítkem zaštiťuje statik. Statika a dynamika jsou jedněmi z oborů, pro které uděluje Česká komora autorizovaných inženýrů a techniků autorizaci. Pro tyto obory lze získat autorizaci ve stupni autorizovaný inženýr pro statiku a dynamiku staveb. Pro navrhování staveb se zvýšenými nároky na statiku a dynamiku, jako jsou mosty, inženýrské konstrukce, nádrže, vysoké komíny a podobně, je třeba autorizování v oboru autorizovaný inženýr pro mosty a inženýrské konstrukce. Součástí tohoto oboru u autorizovaného inženýra je i statika a dynamika staveb.[10]
Odkazy
Reference
- ↑ a b c d Jaroslav Kadlčák, Jiří Kytýr, Statika stavebních konstrukcí I., VUTIUM, Brno 1998, str. 17,18
- ↑ Felix R. Paturi, Kronika techniky, Fortuna print, spol s r. o., Praha 1993, 1. české vydání, str. 32
- ↑ Felix R. Paturi, Kronika techniky, Fortuna print, spol s r. o., Praha 1993, 1. české vydání, str. 43
- ↑ a b Felix R. Paturi, Kronika techniky, Fortuna print, spol s r. o., Praha 1993, 1. české vydání, str. 65
- ↑ a b Felix R. Paturi, Kronika techniky, Fortuna print, spol s r.o., Praha 1993, 1. české vydání, str. 109
- ↑ Max von Laue, Dějiny fyziky, malá moderní encyklopedie, Orbis, Praha 1959, nákl. 17000,1.vydání, str. 19, 20
- ↑ Jaroslav Kadlčák, Jiří Kytýr, Statika stavebních konstrukcí I., VUTIUM, Brno 1998, str. 34
- ↑ Jaroslav Kadlčák, Jiří Kytýr, Statika stavebních konstrukcí I., VUTIUM, Brno 1998, str. 67
- ↑ Jaroslav Kadlčák, Jiří Kytýr, Statika stavebních konstrukcí I., VUTIUM, Brno 1998, str. 20
- ↑ http://www.ckait.cz/content/autorizace-ckait
Související články
Externí odkazy
 Obrázky, zvuky či videa k tématu statika na Wikimedia Commons
Obrázky, zvuky či videa k tématu statika na Wikimedia Commons - stránky o statických posudcích Archivováno 2. 9. 2011 na Wayback Machine.
- příloha č. 1 k vyhlášce č. 499/2006 Sb. o dokumentaci staveb
Média použitá na této stránce
Greek philosopher Archimedes having his famous bath
Beam in static equilibrium: The sum of forces and moment are zero.
- Moments clockwise red
- Moments counterclockwise blue
- Center of rotation pink
Autor: Cyron Ray Macey from Brisbane (-27.470963,153.026505), Australia, Licence: CC BY 2.0
Hot air balloon over Brisbane, Australia.
P6060062
The Fourth Bridge
Force diagram for an static body in a horizontal plane.




