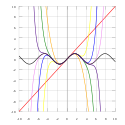
Taylorův rozvoj stupně 1 3 5 7 9 11 13 sin(x) . Sin(x) je vyznačen černě. Taylorova řada je v matematice zvláštní mocninná řada .
Za určitých předpokladů o funkci f(x) v okolí bodu a lze tuto funkci vyjádřit (rozvinout) jako mocninnou řadu. Toto vyjádření funkce prostřednictvím Taylorovy řady se označuje jako Taylorův rozvoj . Pokud se jedná o rozvoj v okolí bodu 0, mluvíme o Maclaurinově řadě .
Pro přibližné vyjádření hodnot funkce není nutné vyjadřovat všechny členy Taylorovy řady, ale můžeme zanedbat členy s vyššími derivacemi. Získáme tím tzv. Taylorův polynom . Taylorův polynom tedy aproximuje hodnoty funkce , která má v daném bodě derivaci , pomocí polynomu , jehož koeficienty závisí na derivacích funkce v tomto bodě.
Řada je pojmenována po anglickém matematikovi Brooku Taylorovi , který ji publikoval v roce 1712, avšak metoda aproximace funkce mocninnou řadou byla objevena již roku 1671 Jamesem Gregorym .
Definice V případě existence všech konečných derivací funkce f {\displaystyle f} a {\displaystyle a}
f ( x ) = f ( a ) + f ′ ( a ) 1 ! ( x − a ) + f ′ ′ ( a ) 2 ! ( x − a ) 2 + f ( 3 ) ( a ) 3 ! ( x − a ) 3 + ⋯ = ∑ k = 0 ∞ f ( k ) ( a ) k ! ( x − a ) k . {\displaystyle f(x)=f(a)+{\frac {f^{\prime }(a)}{1!}}(x-a)+{\frac {f^{\prime \prime }(a)}{2!}}(x-a)^{2}+{\frac {f^{(3)}(a)}{3!}}(x-a)^{3}+\cdots =\sum _{k=0}^{\infty }{\frac {f^{(k)}(a)}{k!}}(x-a)^{k}.} Má-li funkce f {\displaystyle f} a {\displaystyle a} n {\displaystyle n} n {\displaystyle n} f {\displaystyle f} a {\displaystyle a}
T n f , a ( x ) = f ( a ) + f ′ ( a ) 1 ! ( x − a ) + f ′ ′ ( a ) 2 ! ( x − a ) 2 + ⋯ + f ( n ) ( a ) n ! ( x − a ) n = ∑ k = 0 n f ( k ) ( a ) k ! ( x − a ) k , {\displaystyle T_{n}^{f,a}(x)=f(a)+{\frac {f^{\prime }(a)}{1!}}(x-a)+{\frac {f^{\prime \prime }(a)}{2!}}(x-a)^{2}+\cdots +{\frac {f^{(n)}(a)}{n!}}(x-a)^{n}=\sum _{k=0}^{n}{\frac {f^{(k)}(a)}{k!}}(x-a)^{k},} kde nultou derivací je myšlena samotná funkce, tzn. f ( 0 ) = f {\displaystyle f^{(0)}=f} n {\displaystyle n}
Rozvoj funkce f ( x ) {\displaystyle f(x)} a {\displaystyle a} ( n + 1 ) {\displaystyle (n+1)} Taylorovy věty , která říká, že takovéto funkce lze v okolí bodu a {\displaystyle a}
f ( x ) = f ( a ) + f ′ ( a ) 1 ! ( x − a ) + f ′ ′ ( a ) 2 ! ( x − a ) 2 + ⋯ + f ( n ) ( a ) n ! ( x − a ) n + R n + 1 f , a ( x ) . {\displaystyle f(x)=f(a)+{\frac {f^{\prime }(a)}{1!}}(x-a)+{\frac {f^{\prime \prime }(a)}{2!}}{(x-a)}^{2}+\cdots +{\frac {f^{(n)}(a)}{n!}}{(x-a)}^{n}+R_{n+1}^{f,a}(x).} Nechť je funkce φ {\displaystyle \varphi } a {\displaystyle a} c {\displaystyle c}
R n + 1 f , a ( x ) = 1 n ! φ ( x ) − φ ( a ) φ ′ ( c ) f ( n + 1 ) ( c ) ( x − c ) n . {\displaystyle R_{n+1}^{f,a}(x)={\frac {1}{n!}}{\frac {\varphi (x)-\varphi (a)}{\varphi ^{\prime }(c)}}f^{(n+1)}(c)(x-c)^{n}.} Speciálně lze zbytek R n + 1 {\displaystyle R_{n+1}}
R n + 1 f , a ( x ) = f ( n + 1 ) ( c ) ( n + 1 ) ! ( x − a ) n + 1 {\displaystyle R_{n+1}^{f,a}(x)={\frac {f^{(n+1)}(c)}{(n+1)!}}{(x-a)}^{n+1}} tzv. Lagrangeův tvar zbytku , tedy φ ( t ) = ( x − t ) n + 1 {\displaystyle \varphi (t)=(x-t)^{n+1}} R n + 1 f , a ( x ) = 1 n ! f ( n + 1 ) ( c ) ( x − c ) n ( x − a ) {\displaystyle R_{n+1}^{f,a}(x)={\frac {1}{n!}}f^{(n+1)}(c)(x-c)^{n}(x-a)\quad } tzv. Cauchyův tvar zbytku , tedy φ ( t ) = t {\displaystyle \varphi (t)=t}
Taylorova řada funkce f ( x ) {\displaystyle f(x)} konverguje v bodě x {\displaystyle x} f ( x ) {\displaystyle f(x)}
lim n → ∞ R n f , a ( x ) = 0. {\displaystyle \lim _{n\to \infty }R_{n}^{f,a}(x)=0.}
Pro funkci f ( x 1 , … , x n ) {\displaystyle f(x_{1},\ldots ,x_{n})} A = [ a 1 , … , a n ] {\displaystyle A=[a_{1},\ldots ,a_{n}]} totálních diferenciálů jako
f ( x 1 , … , x n ) = f ( a 1 , … , a n ) + d f ( a 1 , … , a n ) 1 ! + d 2 f ( a 1 , … , a n ) 2 ! + ⋯ + d n f ( a 1 , … , a n ) n ! + R n + 1 f , a , {\displaystyle f(x_{1},\ldots ,x_{n})=f(a_{1},\ldots ,a_{n})+{\frac {\mathrm {d} f(a_{1},\ldots ,a_{n})}{1!}}+{\frac {\mathrm {d} ^{2}f(a_{1},\ldots ,a_{n})}{2!}}+\cdots +{\frac {\mathrm {d} ^{n}f(a_{1},\ldots ,a_{n})}{n!}}+R_{n+1}^{f,a},} kde funkci R n + 1 f , a {\displaystyle R_{n+1}^{f,a}} n -tým členem, lze vyjádřit ve tvaru
R n + 1 f , a = d n + 1 f ( a 1 + Θ ( x 1 − a 1 ) , a 2 + Θ ( x 2 − a 2 ) , . . . , a n + Θ ( x n − a n ) ) ( n + 1 ) ! {\displaystyle R_{n+1}^{f,a}={\frac {\mathrm {d} ^{n+1}f(a_{1}+\Theta (x_{1}-a_{1}),a_{2}+\Theta (x_{2}-a_{2}),...,a_{n}+\Theta (x_{n}-a_{n}))}{(n+1)!}}} pro Θ ∈ ( 0 , 1 ) {\displaystyle \Theta \in (0,1)}
Pro a = 0 {\displaystyle a=0} řadu Maclaurinovu , tedy
f ( x ) = f ( 0 ) + ∑ n = 1 ∞ f ( n ) ( 0 ) n ! x n {\displaystyle f(x)=f(0)+\sum _{n=1}^{\infty }{\frac {f^{(n)}(0)}{n!}}x^{n}}
Maclaurinova řada polynomu je tentýž polynom. e x = 1 + x + x 2 2 ! + x 3 3 ! + ⋯ = ∑ k = 0 ∞ x k k ! pro x ∈ ( − ∞ , ∞ ) {\displaystyle \mathrm {e} ^{x}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots =\sum _{k=0}^{\infty }{\frac {x^{k}}{k!}}\;{\mbox{ pro }}x\in (-\infty ,\infty )} a x = 1 + x ln a 1 ! + x 2 ln 2 a 2 ! + x 3 ln 3 a 3 ! + ⋯ = ∑ n = 0 ∞ ( x ln a ) n n ! pro a > 0 , x ∈ ( − ∞ , ∞ ) {\displaystyle a^{x}=1+{\frac {x\ln a}{1!}}+{\frac {x^{2}\ln ^{2}a}{2!}}+{\frac {x^{3}\ln ^{3}a}{3!}}+\cdots =\sum _{n=0}^{\infty }{\frac {{(x\ln a)}^{n}}{n!}}\;{\mbox{ pro }}a>0,x\in (-\infty ,\infty )} 1 1 − x = 1 + x + x 2 + x 3 + ⋯ = ∑ n = 0 ∞ x n pro x ∈ ( − 1 , 1 ) {\displaystyle {\frac {1}{1-x}}=1+x+x^{2}+x^{3}+\cdots =\sum _{n=0}^{\infty }{x^{n}}\;{\mbox{ pro }}x\in (-1,1)} ( 1 + x ) r = 1 + ( r 1 ) x + ( r 2 ) x 2 + ( r 3 ) x 3 + ⋯ = ∑ n = 0 ∞ ( r n ) x n pro r ∈ R , x ∈ ( − 1 , 1 ) , {\displaystyle {(1+x)}^{r}=1+{r \choose 1}x+{r \choose 2}x^{2}+{r \choose 3}x^{3}+\cdots =\sum _{n=0}^{\infty }{r \choose n}x^{n}\;{\mbox{ pro }}r\in \mathbb {R} ,x\in (-1,1),} ( r n ) = ∏ k = 1 n r − k + 1 k = r ⋅ ( r − 1 ) ⋅ ⋅ ⋅ ( r − n + 1 ) n ! {\displaystyle {\binom {r}{n}}=\prod _{k=1}^{n}{\frac {r-k+1}{k}}={\frac {r\cdot (r-1)\cdot \cdot \cdot (r-n+1)}{n!}}} ln ( 1 + x ) = x − x 2 2 + x 3 3 − x 4 4 + x 5 5 − ⋯ = ∑ n = 1 ∞ ( − 1 ) n + 1 x n n pro x ∈ ( − 1 , 1 ⟩ {\displaystyle \ln(1+x)=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+{\frac {x^{5}}{5}}-\cdots =\sum _{n=1}^{\infty }{(-1)}^{n+1}{\frac {x^{n}}{n}}\;{\mbox{ pro }}x\in (-1,1\rangle } ln 1 + x 1 − x = 2 [ x + x 3 3 + x 5 5 + x 7 7 + ⋯ ] = 2 ∑ n = 0 ∞ x 2 n + 1 2 n + 1 x ∈ ( − 1 , 1 ) {\displaystyle \ln {\frac {1+x}{1-x}}=2\left[x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\cdots \right]=2\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}}\;x\in (-1,1)} sin x = x − x 3 3 ! + x 5 5 ! − x 7 7 ! + ⋯ = ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! pro x ∈ ( − ∞ , ∞ ) {\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{(-1)}^{n}{\frac {x^{2n+1}}{(2n+1)!}}\;{\mbox{ pro }}x\in (-\infty ,\infty )} cos x = 1 − x 2 2 ! + x 4 4 ! − x 6 6 ! + ⋯ = ∑ n = 0 ∞ ( − 1 ) n x 2 n ( 2 n ) ! pro x ∈ ( − ∞ , ∞ ) {\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{(-1)}^{n}{\frac {x^{2n}}{(2n)!}}\;{\mbox{ pro }}x\in (-\infty ,\infty )} tg x = x + 1 3 x 3 + 2 15 x 5 + 17 315 x 7 + ⋯ pro x ∈ ( − π 2 , π 2 ) {\displaystyle \operatorname {tg} \,x=x+{\frac {1}{3}}x^{3}+{\frac {2}{15}}x^{5}+{\frac {17}{315}}x^{7}+\cdots \;{\mbox{ pro }}x\in \left(-{\frac {\pi }{2}},{\frac {\pi }{2}}\right)} cotg x = 1 x − 1 3 x − 1 45 x 3 − 2 945 x 5 − ⋯ pro x ∈ ( 0 , π ) {\displaystyle \operatorname {cotg} \,x={\frac {1}{x}}-{\frac {1}{3}}x-{\frac {1}{45}}x^{3}-{\frac {2}{945}}x^{5}-\cdots \;{\mbox{ pro }}x\in (0,\pi )} arcsin x = x + 1 2 x 3 3 + 1 2 3 4 x 5 5 + 1 2 3 4 5 6 x 7 7 + ⋯ = ∑ n = 0 ∞ ( 2 n − 1 ) ! ! ( 2 n ) ! ! x 2 n + 1 2 n + 1 pro x ∈ ⟨ − 1 , 1 ⟩ {\displaystyle \operatorname {arcsin} \,x=x+{\frac {1}{2}}{\frac {x^{3}}{3}}+{\frac {1}{2}}{\frac {3}{4}}{\frac {x^{5}}{5}}+{\frac {1}{2}}{\frac {3}{4}}{\frac {5}{6}}{\frac {x^{7}}{7}}+\cdots =\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}{\frac {x^{2n+1}}{2n+1}}\;{\mbox{ pro }}x\in \langle -1,1\rangle } arccos x = π 2 − arcsin x = π 2 − ∑ n = 0 ∞ ( 2 n − 1 ) ! ! ( 2 n ) ! ! x 2 n + 1 2 n + 1 pro x ∈ ⟨ − 1 , 1 ⟩ {\displaystyle \operatorname {arccos} \,x={\frac {\pi }{2}}-\arcsin \,x={\frac {\pi }{2}}-\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}{\frac {x^{2n+1}}{2n+1}}\;{\mbox{ pro }}x\in \langle -1,1\rangle } arctg x = x − x 3 3 + x 5 5 − x 7 7 + ⋯ = ∑ n = 0 ∞ ( − 1 ) n x 2 n + 1 2 n + 1 pro x ∈ ⟨ − 1 , 1 ⟩ {\displaystyle \operatorname {arctg} \,x=x-{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}-{\frac {x^{7}}{7}}+\cdots =\sum _{n=0}^{\infty }{(-1)}^{n}{\frac {x^{2n+1}}{2n+1}}\;{\mbox{ pro }}x\in \langle -1,1\rangle } sinh x = x + x 3 3 ! + x 5 5 ! + ⋯ = ∑ n = 0 ∞ x 2 n + 1 ( 2 n + 1 ) ! pro x ∈ ( − ∞ , ∞ ) {\displaystyle \sinh x=x+{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{(2n+1)!}}\;{\mbox{ pro }}x\in (-\infty ,\infty )} cosh x = 1 + x 2 2 ! + x 4 4 ! + ⋯ = ∑ n = 0 ∞ x 2 n ( 2 n ) ! pro x ∈ ( − ∞ , ∞ ) {\displaystyle \cosh x=1+{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{2n}}{(2n)!}}\;{\mbox{ pro }}x\in (-\infty ,\infty )} tanh x = x − 1 3 x 3 + 2 15 x 5 − 17 135 x 7 + ⋅ ⋅ ⋅ pro x ∈ ( − π 2 , π 2 ) {\displaystyle \tanh \,x=x-{\frac {1}{3}}x^{3}+{\frac {2}{15}}x^{5}-{\frac {17}{135}}x^{7}+\cdot \cdot \cdot \;{\mbox{ pro }}x\in {\Bigl (}-{\frac {\pi }{2}},{\frac {\pi }{2}}{\Bigr )}} arcsinh x = ∑ n = 0 ∞ ( − 1 ) n ( 2 n ) ! 4 n ( n ! ) 2 ( 2 n + 1 ) x 2 n + 1 pro x ∈ ⟨ − 1 , 1 ⟩ {\displaystyle \operatorname {arcsinh} \,x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}\;{\mbox{ pro }}x\in \langle -1,1\rangle } arctanh x = ∑ n = 0 ∞ x 2 n + 1 2 n + 1 pro x ∈ ( − 1 , 1 ) {\displaystyle \operatorname {arctanh} \,x=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}}\;{\mbox{ pro }}x\in (-1,1)}
Pro výpočet Taylorova polynomu složitějších funkcí se používá několik metod. Dá se počítat přímo z definice, což ale vyžaduje výpočet derivací vyšších řádů, které mohou být složité. Častěji se používá substituce, násobení , dělení, sčítání nebo odčítání Taylorových polynomů známých funkcí.
Chceme spočítat Taylorův polynom řádu 7 v bodě 0 funkce f ( x ) = ln ( cos ( x ) ) {\displaystyle f(x)=\ln(\cos(x))} f ( x ) = ln ( 1 + ( cos ( x ) − 1 ) ) . {\displaystyle f(x)=\ln(1+(\cos(x)-1)).}
Taylorův polynom přirozeného logaritmu je ln ( 1 + z ) = z − z 2 2 + z 3 3 + O ( z 4 ) {\displaystyle \textstyle \ln(1+z)=z-{\frac {z^{2}}{2}}+{\frac {z^{3}}{3}}+O(z^{4})} cos ( x ) = 1 − x 2 2 + x 4 24 − x 6 720 + O ( x 8 ) {\displaystyle \textstyle \cos(x)=1-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}-{\frac {x^{6}}{720}}+O(x^{8})} Landauovu notaci ).
Nyní využijeme substituce vnitřní funkce a vynecháme členy stupně vyššího než 7 díky použití notace velké O:
f ( x ) = ln ( 1 + ( cos x − 1 ) ) = ( cos x − 1 ) − 1 2 ( cos x − 1 ) 2 + 1 3 ( cos x − 1 ) 3 + O ( ( cos x − 1 ) 4 ) = ( − x 2 2 + x 4 24 − x 6 720 + O ( x 8 ) ) − 1 2 ( − x 2 2 + x 4 24 + O ( x 6 ) ) 2 + 1 3 ( − x 2 2 + O ( x 4 ) ) 3 + O ( x 8 ) = − x 2 2 + x 4 24 − x 6 720 − x 4 8 + x 6 48 − x 6 24 + O ( x 8 ) = − x 2 2 − x 4 12 − x 6 45 + O ( x 8 ) . {\displaystyle {\begin{aligned}f(x)&=\ln(1+(\cos \,x-1))=(\cos \,x-1)-{\frac {1}{2}}(\cos \,x-1)^{2}+{\frac {1}{3}}(\cos \,x-1)^{3}+O((\cos \,x-1)^{4})\\&={\Bigl (}-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}-{\frac {x^{6}}{720}}+O(x^{8}){\Bigr )}-{\frac {1}{2}}{\Bigl (}-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}+O(x^{6}){\Bigr )}^{2}+{\frac {1}{3}}{\Bigl (}-{\frac {x^{2}}{2}}+O(x^{4}){\Bigr )}^{3}+O(x^{8})\\&=-{\frac {x^{2}}{2}}+{\frac {x^{4}}{24}}-{\frac {x^{6}}{720}}-{\frac {x^{4}}{8}}+{\frac {x^{6}}{48}}-{\frac {x^{6}}{24}}+O(x^{8})=-{\frac {x^{2}}{2}}-{\frac {x^{4}}{12}}-{\frac {x^{6}}{45}}+O(x^{8}).\end{aligned}}} Na závěr si můžeme všimnout, že koeficienty u x , x 3 , x 5 , x 7 , ⋅ ⋅ ⋅ {\displaystyle x,x^{3},x^{5},x^{7},\cdot \cdot \cdot } kosinus je sudá funkce.
Chceme spočítat Taylorův polynom funkce g ( x ) = e x cos x {\displaystyle \textstyle g(x)={\frac {e^{x}}{\cos \,x}}}
Máme známé Taylorovy polynomy: e x = 1 + x + x 2 2 ! + x 3 3 ! + x 4 4 ! + O ( x 4 ) {\displaystyle \textstyle e^{x}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+O(x^{4})} cos x = 1 − x 2 2 ! + x 4 4 ! + O ( x 4 ) {\displaystyle \textstyle \cos \,x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+O(x^{4})} metodu neurčitých koeficientů .
Předpokládejme, že platí e x cos x = c 0 + c 1 x + c 2 x 2 + c 3 x 3 + c 4 x 4 + ⋅ ⋅ ⋅ {\displaystyle \textstyle {\frac {e^{x}}{\cos \,x}}=c_{0}+c_{1}x+c_{2}x^{2}+c_{3}x^{3}+c_{4}x^{4}+\cdot \cdot \cdot }
e x = ( c 0 + c 1 x + c 2 x 2 + c 3 x 3 + c 4 x 4 ) cos x = ( c 0 + c 1 x + c 2 x 2 + c 3 x 3 + c 4 x 4 ) ( 1 − x 2 2 ! + x 4 4 ! + O ( x 4 ) ) = c 0 − c 0 2 x 2 + c 0 4 ! x 4 + c 1 x − c 1 2 x 3 + c 1 4 ! x 5 + c 2 x 2 − c 2 2 x 4 + c 2 4 ! x 6 + c 3 x 3 − c 3 2 x 5 + c 3 4 ! x 7 + O ( x 4 ) = c 0 + c 1 x + ( c 2 − c 0 2 ) x 2 + ( c 3 − c 1 2 ) x 3 + ( c 4 − c 2 2 + c 0 4 ! ) x 4 + O ( x 4 ) {\displaystyle {\begin{aligned}e^{x}&=(c_{0}+c_{1}x+c_{2}x^{2}+c_{3}x^{3}+c_{4}x^{4})\cos \,x=(c_{0}+c_{1}x+c_{2}x^{2}+c_{3}x^{3}+c_{4}x^{4}){\Bigl (}1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}+O(x^{4}){\Bigr )}\\&=c_{0}-{\frac {c_{0}}{2}}x^{2}+{\frac {c_{0}}{4!}}x^{4}+c_{1}x-{\frac {c_{1}}{2}}x^{3}+{\frac {c_{1}}{4!}}x^{5}+c_{2}x^{2}-{\frac {c_{2}}{2}}x^{4}+{\frac {c_{2}}{4!}}x^{6}+c_{3}x^{3}-{\frac {c_{3}}{2}}x^{5}+{\frac {c_{3}}{4!}}x^{7}+O(x^{4})\\&=c_{0}+c_{1}x+{\Bigl (}c_{2}-{\frac {c_{0}}{2}}{\Bigr )}x^{2}+{\Bigl (}c_{3}-{\frac {c_{1}}{2}}{\Bigr )}x^{3}+{\Bigl (}c_{4}-{\frac {c_{2}}{2}}+{\frac {c_{0}}{4!}}{\Bigr )}x^{4}+O(x^{4})\end{aligned}}} Porovnáním s koeficienty Taylorova polynomu exponenciální funkce dostáváme řešení
e x cos x = 1 + x + x 2 + 2 3 x 3 + x 4 2 + O ( x 4 ) {\displaystyle {\frac {e^{x}}{\cos \,x}}=1+x+x^{2}+{\frac {2}{3}}x^{3}+{\frac {x^{4}}{2}}+O(x^{4})}
Odkazy
Reference V tomto článku byl použit překlad textu z článku Taylor series
Literatura Rektorys Karel a kol.: Přehled užité matematiky I. . Prometheus, Praha, 2003 , 7. vydání. ISBN 80-7196-179-5 Tkadlec Josef: Diferenciální a integrální počet funkcí jedné proměnné . Nakladatelství ČVUT, Praha 2004 , 1. vydání. ISBN 80-01-03039-3 Krbálek Milan: Matematická analýza III . Nakladatelství ČVUT, Praha 2008 , 2. vydání.

 Obrázky, zvuky či videa k tématu Taylorova řada na Wikimedia Commons
Obrázky, zvuky či videa k tématu Taylorova řada na Wikimedia Commons