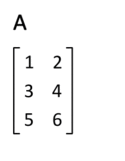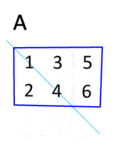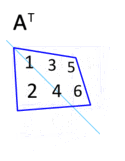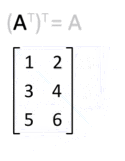
Transpozice matice

V lineární algebře se matice, která vznikne z matice vzájemnou výměnou řádků a sloupců, nazývá matice transponovaná k matici a obvykle se značí . [1] Odpovídající operace je tzv. transpozice matice.
Transpozici matice zavedl v roce 1858 britský matematik Arthur Cayley. [2] Reprezentuje-li matice binární relaci, pak její transpozice odpovídá inverzní relaci.
Definice
Matici transponovanou k matici lze získat libovolnou z následujících metod:
- Převrácením podél její hlavní diagonály nebo
- zápisem řádků do sloupců nebo
- zápisem sloupců do řádků .
Formálně, pro jednotlivé prvky transponované matice platí:
Pokud má matice rozměry , pak její transpozicí vznikne matice o rozměrech .
Symbol je rezervován pro označení transpozice a neměl by být zaměňován s jiným významem horního indexu, jako např. název proměnné ve výrazu , znamenajícím -tou mocninu čtvercové matice .
Ukázky
- Transpozicí matice vznikne .
Definice matic využívající transpozici
Čtvercová matice, jenž je rovna své transpozici, se nazývá symetrická matice; čili je symetrická, pokud
- .
Čtvercová matice, jenž je rovna záporu své transpozice, se nazývá antisymetrická matice; čili je antisymetrická, pokud
- .
Čtvercová komplexní matice, jejíž transpozice je rovna matici, kde každý prvek je nahrazen k němu komplexně sdruženým číslem, se nazývá hermitovská matice; čili je hermitovská, pokud
- .
Čtvercová matice, jejíž transpozice se shoduje s její inverzní matici, se nazývá ortogonální matice; čili je ortogonální, pokud
- .
Vlastnosti
- Dvojitá transpozice matice je opět původní matice:
- ,
- neboli operace transpozice je involuce.
- Skalární násobek lze vytknout před operaci transpozice:
- neboli transpozice zachovává skalární násobek matic.
- Transpozice součtu matic je součtem transponovaných matic:
- neboli transpozice zachovává součet matic.
- Transpozice součinu dvou matic je součinem transponovaných matic v obráceném pořadí:
- Indukcí lze tento vztah rozšířit na součin více matic:
- Z předchozího vztahu vyplývá, že čtvercová matice je regulární, právě když je regulární . V tomto případě platí, že transpozice inverzní matice je rovna inverzi transponované matice:
- Skalární součin dvou reálných sloupcových vektorů a lze spočítat jako jediný prvek maticového součinu:
- Determinant čtvercové matice se transpozicí nezmění:
- Vlastní čísla čtvercové matice se shodují s vlastními čísly její transpozice , protože obě matice mají totožný charakteristický polynom.
- Pro libovolnou matici platí, že obě matice i jsou symetrické. Symetrie matice prostě plyne ze skutečnosti, že je sama sobě transpozicí:
- .
- Je-li navíc reálná matice, pak obě matice i jsou pozitivně semidefinitní.
Implementace maticové transpozice na počítačích

Na počítači se lze často vyhnout výpočtu a ukládání transpozice matice v paměti pouhým přístupem ke stejným datům, ale jen v jiném pořadí. Například softwarové knihovny pro lineární algebru, jako je BLAS, obvykle poskytují možnosti, jak určit, že určité matice mají být interpretovány v transponovaném pořadí, aby se předešlo nutnosti přesunu dat.
V řadě případů je však nutné nebo žádoucí fyzicky přeuspořádat matici v paměti na její transpozici. Například s maticí uloženou v pořadí po řádcích jsou řádky matice v paměti souvislé a sloupce nesouvislé. Pokud je třeba provádět opakované operace se sloupci, například v rychlé Fourierově transformaci, může transpozice matice v paměti (aby sloupce byly souvislé) zrychlit výpočet díky principu lokality paměti.
Ve výpočtech je vhodné provádět transpozici matici s minimálními dodatečnými paměťovými nároky. To vede k problému transpozice matice typu na místě, neboli s dodatečnou pamětí konstantní velikosti, případně o velikosti mnohem menší než udává součin odpovídající alokaci paměti pro celou transponovanou matici. V případě, že , jde o složitou permutaci uložených dat, jejíž implementace na místě není triviální. Efektivní transpozice matice na místě se stala předmětem četných výzkumných publikací v teoretické informatice už koncem 50. let 20. století.
Odkazy
Reference
V tomto článku byl použit překlad textu z článku Transpose na anglické Wikipedii.
- ↑ ČSN EN ISO 80000-2 (011300). Veličiny a jednotky - Část 2: Matematika. Česká agentura pro standardizaci, 2020-11-01. detail.
- ↑ Arthur Cayley (1858) "A memoir on the theory of matrices", Philosophical Transactions of the Royal Society of London, 148 : 17–37. Matice transponovaná (neboli "transpozice") je definována na str. 31.
Literatura
- Slovník školské matematiky. Praha: SPN, 1981. 240 s.
- BÄRTSCH, Hans-Jochen. Matematické vzorce. Praha: Academia, 2006. 832 s. ISBN 80-200-1448-9. Kapitola Matice, s. 180–198.
- HLADÍK, Milan. Lineární algebra (nejen) pro informatiky. 1.. vyd. Praha: Matfyzpress, 2019. 328 s. ISBN 978-80-7378-378-5.
- OLŠÁK, Petr. Lineární algebra [online]. Praha: 2007 [cit. 2023-02-20]. Dostupné online.
Související články
Externí odkazy
- Eduard Krajník - Maticový počet Archivováno 26. 7. 2020 na Wayback Machine.
Média použitá na této stránce
The transpose of a matrix can be obtained by reflecting the elements along the main diagonal. Transposing twice returns the matrix to the original form. This process is illustrated in the animation, albeit with an equivalent and more intuitive rotation in 3D space.