Trojúhelník
Trojúhelník (symbol △) je základní geometrický útvar, který má tři vrcholy a tři strany. V euklidovské geometrii jakékoliv tři body neležící v jedné přímce určují právě jeden trojúhelník a právě jednu rovinu v dvourozměrném euklidovském prostoru (2D). Trojúhelník s vrcholy A, B, C označujeme , proti vrcholům leží strany a, b, c, vnitřní úhly označujeme řeckými písmeny (α, β, γ). Součet vnitřních úhlů takového trojúhelníku je roven 180° (tj. π v obloukové míře). Pokud není uvedeno jinak, týká se článek pouze Euklidovské geometrie a Euklidovské roviny.
Mimo euklidovskou geometrii existuje sférický trojúhelník na kulové ploše (např. dostatečně velký trojúhelník vyznačený na povrchu zeměkoule), který má součet velikostí vnitřních úhlů vždy větší než 180° a trojúhelník v hyperbolické (Lobačevského) rovině (tj. trojúhelník na vnitřním povrchu koule) vždy menší než 180°.
Základní pojmy


vnější úhly: α’, β’, γ’ a α’’, β’’, γ’’
Úsečky, které spojují vrcholy, se nazývají strany trojúhelníku. Úhly, které svírají strany, se nazývají vnitřní úhly trojúhelníku. Vedlejší úhly k vnitřním úhlům se nazývají vnější úhly trojúhelníka (u každého vrcholu jsou dva, vnější úhel je doplněk vnitřního úhlu do 180°).[1] Každý trojúhelník má 3 strany, 3 vnitřní úhly, 6 vnějších úhlů. Trojúhelník nemá úhlopříčky.
Označíme-li vrcholy trojúhelníka velkými tiskacími písmeny A, B, C, pak trojúhelník označujeme jako . Takový trojúhelník má strany označené malými písmeny a, b, c tak, že stejnojmenná strana leží vždy proti stejně označenému vrcholu (tj. proti vrcholu A leží strana a, proti vrcholu B leží strana b atd.). Vnitřní úhly se označují popořadě řeckými písmeny (tj. u vrcholu A leží vnitřní úhel α, u vrcholu B leží β, u vrcholu C leží γ). Podobně se postupuje při označení trojúhelníka jinými písmeny, např. . Při označení trojúhelníka má význam pořadí stran (jedná se obvykle o různé trojúhelníky), což se využívá například u podobnosti trojúhelníků.
Druhy trojúhelníků
Eukleidés napsal již před dvěma tisíci lety knihu Základy, kde popisuje trojúhelník jako jeden ze základních geometrických elementů. Druhy trojúhelníků jsou od té doby buď přímými překlady z řečtiny nebo latiny.
Podle stran
Euklidés definoval podle délky stran tři druhy trojúhelníků:
- Obecný trojúhelník (též různostranný) – žádné dvě strany nejsou shodné (řecky σκαληνὸν, čti skalinón, znamená nestejné)
- Rovnoramenný trojúhelník – dvě strany jsou navzájem shodné, ale nejsou shodné s třetí stranou (řecky ἰσοσκελὲς, čti isoskelés, znamená stejné nohy)
- Rovnostranný trojúhelník – všechny strany jsou shodné (řecky ἰσόπλευρον, čti isópleuron, znamená stejné strany)
- Obecný t.
- Rovnostranný t.
- Rovnoramenný t.
Podle úhlů
- Ostroúhlý trojúhelník – všechny vnitřní úhly jsou ostré
- Pravoúhlý trojúhelník – jeden vnitřní úhel je pravý, zbývající dva jsou ostré
- Tupoúhlý trojúhelník – jeden vnitřní úhel je tupý, zbývající dva jsou ostré
- Ostroúhlý t.
- Pravoúhlý t.
- Tupoúhlý t.
Obvod a obsah
Obvod trojúhelníku o vypočteme jako součet všech jeho stran:
- , kde , , jsou strany trojúhelníku
Obsah trojúhelníku S se vypočte jako polovina součinu libovolné strany a k ní příslušné výšky:
- , kde je výška příslušná straně a
Pokud není známá příslušná výška, je možné obsah trojúhelníku vypočítat podle Heronova vzorce
- , kde je obvod trojúhelníku
Obsah trojúhelníku pomocí poloměru kružnice opsané ():
Obsah trojúhelníku pomocí poloměru kružnice vepsané ():
Obsah trojúhelníku pomocí vnitřního úhlu:

Obsah obecného trojúhelníku v rovině kde (ax,ay), (bx,by), (cx,cy) jsou souřadnice vrcholů (vychází z vektorového součinu, použití hlavně v grafice):
nebo:
Použije-li se předcházející vzorec bez absolutní hodnoty, lze jej využít pro ověření zda bod (dx,dy) leží uvnitř trojúhelníku ABC. V případě, že leží, tak znaménka obsahů všech čtyř trojúhelníků ABC, ABD, BCD a CAD jsou stejná. Leží-li vně, nemají všechny obsahy stejné znaménko. To je kladné, obíhají-li vrcholy ve směru hodinových ručiček.
Věty o trojúhelníku
V pravoúhlém trojúhelníku platí:
- Pythagorova věta (c² = a² + b²)
V jakémkoliv obecném trojúhelníku platí:
- sinová věta
- kosinová věta (zobecnění Pythagorovy věty na nepravoúhlý trojúhelník)
- tangentová věta
Vlastnosti trojúhelníku
Trojúhelníková nerovnost
Strany trojúhelníku splňují větu o trojúhelníkové nerovnosti. Součet dvou libovolných stran trojúhelníku je vždy delší než strana třetí, neboli:
- a + b > c
- a + c > b
- b + c > a
- a + c > b
Součet úhlů
Součet všech vnitřních úhlů je v každém trojúhelníku 180°. Součet vnitřního a příslušného vnějšího úhlu je 180°. Součet dvou vnitřních úhlů se rovná vnějšímu úhlu u zbývajícího vrcholu. Proti většímu úhlu leží větší strana.
- α + α’ = β + β’ = γ + γ’ = 180°
- α + β = γ’
- α + γ = β’
- β + γ= α’
- α + γ = β’
- α + β + γ = 180°
- α’ + β’ + γ’ = 360°
Zavedeme-li veličinu , pak lze velikosti vnitřních úhlů určit ze vztahů
Souměrnost
Obecný trojúhelník není osově ani středově souměrný, některé druhy trojúhelníků mohou být osově souměrné např.: rovnoramenný a rovnostranný trojúhelník.
Výška

Výška je úsečka, jejímiž krajními body jsou vrchol trojúhelníku a pata kolmice vedené tímto vrcholem na protější stranu, resp. přímku na níž protější strana leží (nebo, stručněji řečeno, kolmice z vrcholu na protější stranu, resp. přímku na níž protější strana leží). Průsečík výšky s příslušnou stranou se nazývá pata výšky. Každý trojúhelník má tři výšky.
Přímky, na nichž leží výšky, se protínají v jednom bodě, který se nazývá ortocentrum. Ortocentrum leží buď uvnitř trojúhelníku, pokud je ostroúhlý, nebo u pravoúhlého trojúhelníka splývá s jeho vrcholem, při němž je pravý úhel, anebo leží vně, je-li to trojúhelník tupoúhlý.
Spojnice jednotlivých pat výšek tvoří ortický trojúhelník. Pravoúhlý trojúhelník svůj ortický trojúhelník nemá, protože jeho dvě paty výšek splývají.
Ortocentrum tupoúhlého trojúhelníku je středem jedné z kružnic připsaných jeho ortickému trojúhelníku.
Výšky se označují malým písmenem v s dolním indexem příslušné strany.
Pro výšky trojúhelníku platí: , čili: , kde S je plocha trojúhelníka.
Velikosti výšek jsou určeny vztahy
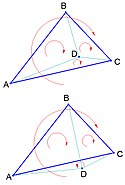
Těžnice

Těžnice je úsečka, jejímiž krajními body jsou střed strany a protilehlý vrchol trojúhelníku. Každý trojúhelník má tři těžnice. Těžnice se protínají v jednom bodě, který se nazývá těžiště. Těžiště rozděluje každou těžnici na dva díly v poměru 2 : 1, přitom vzdálenost těžiště od vrcholu je dvojnásobek vzdálenosti od středu protější strany. Každá těžnice rozděluje trojúhelník na dva díly se stejným obsahem. Těžnice se označují malým písmenem t s dolním indexem příslušné strany, těžiště se označuje písmenem T. Těžiště a dva vrcholy trojúhelníku tvoří postupně tři trojúhelníky (ABT, ACT, CBT), všechny tři mají stejný obsah.
Souřadnice těžiště lze vypočítat ze souřadnic bodů A,B,C podle vztahu:
Délky těžnic jsou
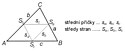
Střední příčka

Střední příčka je spojnice středů dvou stran (dvou pat těžnic). Každý trojúhelník má tři střední příčky. Střední příčka je rovnoběžná s příslušnou stranou a má velikost poloviny příslušné strany. Střední příčky dohromady rozdělují trojúhelník na čtyři shodné trojúhelníky – příčkový trojúhelník a tři trojúhelníky při jednotlivých vrcholech. Těžiště trojúhelníku je zároveň těžištěm jeho příčkového trojúhelníku. Střední příčky se označují malým písmenem s.
Symediána
Symediána je osově souměrný obraz těžnice podle osy příslušného úhlu (např. symediána těžnice z vrcholu A podle osy úhlu při vrcholu A). Každý trojúhelník má tři symediány. Všechny symediány trojúhelníku se protínají v jednom bodě, který se nazývá Lemoinův bod. Lemoinův bod leží uvnitř trojúhelníku a platí pro něj, že má ze všech vnitřních bodů trojúhelníku nejmenší součet čtverců vzdáleností od stran trojúhelníku. Pokud Lemoinovým bodem vedeme rovnoběžky s jednotlivými stranami, všechny průsečíky těchto rovnoběžek se stranami (je jich šest) leží na kružnici, která se nazývá první Lemoinova kružnice. Střed první Lemoinovy kružnice je středem úsečky spojující Lemoinův bod a střed kružnice opsané.
Osy úhlů

Osa vnitřního úhlu dělí na polovinu vnitřní úhel a současně protější stranu dělí v poměru délek přilehlých stran. Osa vnějšího úhlu dělí na polovinu vnější úhel. Na obrázku je osa vnitřního úhlu , osa vnějšího úhlu a také těžnice a výška z vrcholu . Podobně lze získat osy i u ostatních vrcholů.
Třetiny úhlů

Pokud jednotlivé vnitřní úhly rozdělíme přímkami na tři stejné díly (trisekce úhlu), průsečíky těchto přímek (vždy těch dvou, které jsou bližší dané straně trojúhelníku) vždy tvoří rovnostranný trojúhelník (Morleyova věta).
Osy stran
Osa strany je kolmice vedená ze středu strany. Osy stran se protínají v jednom bodě (tento bod má stejnou vzdálenost od všech tří vrcholů trojúhelníka).
Eulerova přímka
Eulerova přímka je přímka, která prochází těžištěm a ortocentrem a středem opsané kružnice. Na Eulerově přímce leží i střed kružnice opsané a střed kružnice devíti bodů. V rovnostranném trojúhelníku těžiště a ortocentrum splývají, takový trojúhelník Eulerovu přímku nemá.
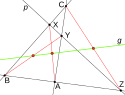
Gaussova přímka

Pokud přímka p protíná přímky, na nichž leží strany obecného trojúhelníku, v bodech X, Y, Z, pak středy úseček AX, BY, CZ leží na přímce. Tato přímka g se nazývá Gaussova přímka.
Kružnice opsaná

Kružnice opsaná trojúhelníku je kružnice, která prochází všemi vrcholy trojúhelníku. Každému trojúhelníku lze opsat kružnici. Střed kružnice opsané leží v průsečíku os stran, poloměr se rovná vzdálenosti středu od libovolného vrcholu. Spojnice středu kružnice opsané a jednotlivých vrcholů trojúhelníku jsou kolmé k jednotlivým stranám jeho ortického trojúhelníku (tzv. Nagelova věta).
Velikost poloměru opsané kružnice určuje vztah
Kružnice vepsaná

Kružnice vepsaná trojúhelníku je kružnice, která se dotýká všech stran trojúhelníku. Každému trojúhelníku lze vepsat kružnici. Střed kružnice vepsané leží v průsečíku os vnitřních úhlů, poloměr se rovná kolmé vzdálenosti středu od libovolné strany.
Pro poloměr kružnice vepsané platí
Vzdálenost mezi středy kružnice vepsané a opsané je
Kružnice připsaná
Kružnice připsaná trojúhelníku je kružnice, která se dotýká jedné strany trojúhelníku a dvou přímek, které jsou prodloužením zbývajících stran trojúhelníku. Střed kružnice připsané leží v průsečíku osy jednoho vnitřního úhlu a dvou vedlejších úhlů při zbývajících dvou vrcholech. Každý trojúhelník má tři kružnice připsané.
Kružnice devíti bodů
Na kružnici devíti bodů leží středy stran, paty výšek a středy spojnic vrcholů se společným průsečíkem výšek. Také se dotýká kružnice vepsané a kružnic připsaných.
Konstrukce trojúhelníku
Trojúhelník může být určen:
- (sss) délkou všech tří stran,
- (sus) délkou dvou stran a velikostí úhlu, který svírají,
- (usu) délkou strany a velikostí úhlů, které k ní přiléhají,
- (Ssu) délkou dvou stran a velikostí úhlu proti větší z nich.[2]
Ke konstrukci trojúhelníku se mohou použít i výšky, těžnice atd.
Odkazy
Literatura
- ŠVRČEK, Jaroslav; VANŽURA, Jiří. Geometrie trojúhelníka. Praha: Nakladatelství technické literatury, 1988.
Reference
- ↑ KRYNICKÝ, Martin. Vnitřní a vnější úhly trojúhelníku I. [online]. Realisticky.cz, 2013-04-03 [cit. 2023-03-06]. Dostupné online.
- ↑ Konstrukce trojúhelníků: věty sss, sus, usu, Ssu – Procvičování online – Umíme matiku. www.umimematiku.cz [online]. [cit. 2023-06-26]. Dostupné online.
Související články
- Pravoúhlý trojúhelník
- Matematika
- Geometrie
- Planimetrie – rovinné geometrické útvary
- Geometrický útvar
- Věty o shodnosti trojúhelníku
Externí odkazy
 Obrázky, zvuky či videa k tématu trojúhelník na Wikimedia Commons
Obrázky, zvuky či videa k tématu trojúhelník na Wikimedia Commons  Téma Trojúhelník ve Wikicitátech
Téma Trojúhelník ve Wikicitátech Slovníkové heslo trojúhelník ve Wikislovníku
Slovníkové heslo trojúhelník ve Wikislovníku- Výpočet úhlů a stran pravoúhlého trojúhelníku
- Základní konstrukce v trojúhelníku – flashová animace sestrojení výšek, těžnic, kružnic opsané a vepsané
Média použitá na této stránce
Těžnice trojúhelníka
Kružnice opsaná trojúhelníku
Výšky trojúhelníka
Autor: Petr K, Licence: CC BY-SA 3.0
Trojúhelník s popsanými vrcholy, stranami a vnitřními úhly.
Autor: Petr K, Licence: CC BY-SA 3.0
Trojúhelník s popsanými vnitřními a vnějšími úhly
Kružnice vepsaná trojúhelníku
An equilateral triangle.
Osy trojúhelníku.
Střední příčky trojúhelníka
Autor: Xerostomus, Licence: CC BY-SA 4.0
Gaussova přímka s popiskami
Autor: Dave3457, Licence: CC BY-SA 3.0
Each of the sides of a triangle are subtended by the angles opposite them.
Autor:
- Morley_triangle.png: Dbenbenn
- derivative work: Hagman (talk)
An illustration of Morley's trisector theorem
Autor: Syp, Licence: Copyrighted free use
Un triangle acutangle est un triangle dont tous ces cotés sont aigus