Václav Chvátal

prof. Václav Chvátal, Ph.D.
Václav Chvátal (2020)
Narození	20. července 1946 (78 let) Habartov Československo Československo
Alma mater	Univerzita ve Waterloo Univerzita Karlova
Pracoviště	Concordia University Montréalská univerzita
Obory	kombinatorika, teorie grafů a kombinatorická optimalizace
Ocenění	Frederick W. Lanchester Prize (2007) John von Neumann Theory Prize (2015)
Některá data mohou pocházet z datové položky.

Václav Chvátal (* 20. července 1946) je emeritním profesorem na univerzitě Concordia v Montrealu v Kanadě a hostujícím profesorem na Karlově univerzitě. Mezi hlavní obory jeho vědecké činnosti patří teorie grafů, kombinatorika a kombinatorická optimalizace.

Narodil se v Praze v roce 1946 a matematické vzdělání získal na Karlově univerzitě, kde studoval pod vedením Zdeňka Hedrlína.^[1] Tři dny po invazi sovětských vojsk v roce 1968 emigroval do Kanady. Na podzim 1970 dokončil doktorské studium (titul Ph.D.) na University of Waterloo.^[2] Působil na McGillově univerzitě (1971 a 1978-1986), Stanfordově univerzitě (1972 a 1974-1977), Université de Montréal (1972-1974 a 1977-1978) a Rutgersově univerzitě (1986-2004), načež se navrátil do Montrealu, kde na Concordia University získal „kanadskou výzkumnou profesuru pro kombinatorickou optimalizaci“ (Canada Research Chair in Combinatorial Optimization)^[3][4] na období 2004-2011. Tu mu pak Kanadská rada pro výzkum v oblasti přírodních věd a inženýrství (Natural Sciences and Engineering Research Council of Canada) obnovila na dalších sedm let jakožto „kanadskou výzkumnou profesuru pro diskrétní matematiku“ (Canada Research Chair in Discrete Mathematics), ale Chvátal se jí vzdal v roce 2014, kdy odešel z osobních důvodů do důchodu.

V roce 2003 mu Université de la Méditerranné udělila čestný doktorát a v roce 2015 mu Institute for Operations Research and the Management Sciences udělil cenu Johna von Neumanna za teorii (John von Neumann Theory Prize).^[5]

Chvátal objevil teorii grafů v plzeňském obchodě „Sovětskaja kniga“ (Сoвeтская Kнигa) v roce 1964 ^[6] a velká část jeho práce se týká grafů.

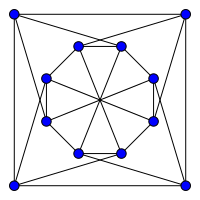
První článek (o grafech) vydal v 19 letech.^[7] Roku 1970 sestrojil nejmenší možný čtyřbarevný a 4-regulární graf bez trojúhelníků, tzv. Chvátalův graf.^[1][8] Článek A note on Hamiltonian circuits z roku 1972^[9] mu vynesl Erdősovo číslo 1: Když graf nemá nezávislou množinu větší než je jeho vrcholová souvislost, tak je ten graf hamiltonovský. Tuto větu dokázali Erdős a Chvátal během 120kilometrové cesty autem a v článku poděkovali řidičce za plynulou jízdu. V článku Tough graphs and hamiltonian circuits z roku 1973^[10] zavedl Chvátal pojem tuhosti grafu (graph toughness), který se váže k existenci hamiltonovských kružnic. Graf je t-tuhý, když pro každé k větší než 1 zanechá odstranění méně než tk uzlů ve zbývajícím podgrafu méně než k souvislých komponent. Například v případě hamiltonovského grafu odstranění jakékoli neprázdné množiny uzlů rozbije tento graf na nejvýš tolik kusů, kolik bylo odstraněných uzlů, a tak jsou hamiltonovské grafy 1-tuhé. Chvátal vyslovil domněnku, že 3/2-tuhé grafy (a později že 2-tuhé grafy) jsou vždycky hamiltonovské; na tyto domněnky jsou protipříklady, ale není známo, zda nějaká konstantní dolní mez na tuhost zaručuje, že graf je hamiltonovský.^[11]

Některé z Chvátalových prací se týkají systémů množin neboli hypergrafů. V hypotéze z roku 1972 – kterou Erdős nazval „překvapivou“ a „krásnou“^[12] a která zůstává otevřena (Chvátal za její řešení nabídnul $10),^[13][14] – Chvátal naznačil, že v každém systému množin uzavřenému pod operací tvorby podmnožin může být největší podsystém vzájemně se protínajících se množin vždy vytvořen volbou jednoho bodu a následujícím výběrem všech množin, které tento bod obsahují. V roce 1979 zobecnil předchozí výsledky Davida Johnsona (J. Comp. Sys. Sci. 1974) a László Lovásze (Discrete Math. 1975) týkající se aproximačního algoritmu pro problém set cover.^[15]

Pod vlivem Jacka Edmondse ve Waterloo se začal Chvátal zajímat o lineární programování.^[1] Brzy si uvědomil důležitost sečných nadrovin pro problémy kombinatorické optimalizace jako je hledání největší nezávislé množiny a zavedl pojem cutting-plane proof.^{[16][17][18][19]} Na Stanfordu v sedmdesátých letech začal psát svou populární učebnici Linear Programming, vydanou v roce 1983.^[1]

Sečných nadrovin užívá také metoda branch and cut v počítačových programech k řešení problému obchodního cestujícího. Mezi lety 1988 a 2005 David Applegate, Robert Bixby, Vašek Chvátal a William Cook napsali jeden takový program, Concorde.^[20][21] V roce 2000 dostal jejich kolektiv cenu The Beale-Orchard-Hays Prize for Excellence in Computational Mathematical Programming za desetistránkový článek On the Solution of Traveling Salesman Problems^[22] popisující několik zdokonalení metody „branch and cut“, která vedla Concorde k řešení případu s 13 509 městy, a v roce 2007 dostal tento kolektiv cenu Frederick W. Lanchester Prize za knihu The Traveling Salesman Problem: A Computational Study.

Chvátal je také znám

• větou art gallery theorem,^{[23][24][25][26]}
• prací na Kolakoského posloupnosti,^[27][28]
• Chvátal–Sankoff konstantami, které se vztahují k průměrné délce nejdelší společné podposloupnosti dvou posloupností,^[29]
• spoluprací s Endrem Szemerédim na těžkých příkladech pro rezoluci,^[30]
• a je zahrnut do Stanfordského celosvětového seznamu 2% úhrnně nejcitovanějších vědců.^[31]

• Vašek Chvátal. Linear Programming. [s.l.]: W.H. Freeman, 1983. Dostupné online. ISBN 978-0-7167-1587-0. Je zde použita šablona {{Cite book}} označená jako k „pouze dočasnému použití“.
• C. Berge and V. Chvátal (eds.). Topics on Perfect Graphs. [s.l.]: Elsevier, 1984. ISBN 978-0-444-86587-8. Je zde použita šablona {{Cite book}} označená jako k „pouze dočasnému použití“.
• David L. Applegate; Robert E. Bixby; Vašek Chvátal; William J. Cook. The Traveling Salesman Problem: A Computational Study. [s.l.]: Princeton University Press, 2007. Dostupné online. ISBN 978-0-691-12993-8. Je zde použita šablona {{Cite book}} označená jako k „pouze dočasnému použití“.
• Vašek Chvátal (ed.). Combinatorial Optimization: Methods and Applications. [s.l.]: IOS Press, 2011. Dostupné online. ISBN 978-1-60750-717-8. Je zde použita šablona {{Cite book}} označená jako k „pouze dočasnému použití“.
• Vašek Chvátal. Discrete Mathematical Charms of Paul Erdős. A Simple Introduction. [s.l.]: Cambridge University Press, 2021. Dostupné online. ISBN 978-1-108-92740-6. Je zde použita šablona {{Cite book}} označená jako k „pouze dočasnému použití“.

• Obrázky, zvuky či videa k tématu Václav Chvátal na Wikimedia Commons
• Seznam děl v Souborném katalogu ČR, jejichž autorem nebo tématem je Václav Chvátal