Vědecký zápis čísel

Avogadrova konstanta zobrazená kalkulátorem ve vědeckém zápisu, na 3 platné číslice

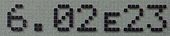
Vědecký zápis čísel nebo vědecká notace je způsob reprezentace čísel na kalkulačkách nebo čísel v pohyblivé řádové čárce na počítačích. Číslo se zapisuje ve tvaru

aEb

(např. 1.23E25, nebo 7.5E-12), kde a je desetinné číslo nazývané mantisa, b je celé číslo nazývané charakteristika čísla, případně exponent.

Pokud typografické nebo technické možnosti dovolují, zapisuje se číslo ve tvaru

${\displaystyle a\times 10^{b}}$,

který se blíží standardnímu matematickému zápisu

${\displaystyle a.10^{b}}$

Některé kalkulačky používají tak zvanou inženýrskou notaci, u které je exponent dělitelný třemi a absolutní hodnota mantisy v intervalu <1, 1000). Tento zápis odpovídá požadavku na vyjadřování fyzikálních hodnot pokud možno v jednotkách, které jsou celočíselnými mocninami čísla tisíc, tj. miliontina, tisícina, tisíc, milion, miliarda, bilion, atd., pro které se používají předpony, u nichž je mocnina desítky dělitelná třemi (mikro, mili, kilo, mega, giga, atd.).

Výhody zápisu

Výhodou zápisu je, že čísla, která by bylo třeba vyjádřit pomocí mnoha míst před nebo za desetinnou čárkou a která obvykle ani nejsou daná s velkou přesností, lze zapsat v krátké formě.

Pravidla zápisu

Mantisa je číslo v rozmezí od 1 (včetně) do 10 (vyjma), exponent rozsahem omezený není. Omezení mantisy není nezbytně nutné pro jednoznačnost zápisu čísel, ale zápisy, které jej splňují jsou praktičtější. Nazývají se normalizované. Exponent umocňuje číslo 10, protože desítka je základem běžně užívané desítkové soustavy.

Mantisa bývá libovolné desetinné číslo, ale exponent může být pouze číslo celé. Tím je zaručeno, že exponent určuje počet číslic, o který se v zápisu posune desetinná čárka (při kladném exponentu vpravo, při záporném vlevo) v mantise, pokud bychom číslo chtěli zapsat běžným způsobem. Jak mantisa, tak exponent mohou být čísla kladná i záporná. Záporná mantisa znamená, že číslo je menší než 0. Záporný exponent (u normalizovaných zápisů) znamená, že číslo leží v otevřeném intervalu (−1, 1). Kladný exponent znamená, že číslo je absolutní hodnotě větší než 10.

Mantisa může být nejen reálné číslo, ale i komplexní. Pro obě složky lze sice použít sdružený zápis, ale u řádových rozdílů obou složek lze pro přesnost použít dva oddělené zápisy. Na druhou stranu se tak ale ztrácí názornost porovnání velikosti obou čísel. Pro dekadický exponent se komplexní hodnoty nepoužívají.

Význam mantisy a exponentu

Význam exponentu spočívá v tom, že je velmi snadné u dvou čísel zjistit, o kolik řádů se liší. Stačí od sebe exponenty odečíst. Význam mantisy spočívá v tom, že lze snadno zjistit, kolikrát je jedno číslo větší než druhé za předpokladu, že mají stejné exponenty. Pokud nemají a přesto je potřeba zjistit, kolikrát je jedno číslo větší než druhé, je potřeba zápis jednoho z čísel převést na takový, který má stejný exponent jako druhý. Takový zápis ale je nenormalizovaný, protože mantisa bude větší nebo rovna 10, nebo menší než 1. Výjimečně se tedy lze zejména z důvodu nutnosti snadného porovnávání čísel setkat s nenormalizovaným zápisem, jehož mantisa toto pravidlo nedodržuje.

Mantisa obvykle nekončí nulou, ale končit může, pokud tato nula vyjadřuje například vyšší přesnost naměřené hodnoty nějaké veličiny.

Pro vědecký zápis čísel se někdy používá i názvu semilogaritmický tvar.^[1] Zápis čísla v semilogaritmickém tvaru nemusí nutně obsahovat mocněnce 10, ale třeba 2. Takové zápisy se využívají v číslicových počítačích při reprezentaci reálných čísel.

Jiné formy zápisu

V některých případech se lze setkat i s vědeckým zápisem čísel v trochu jiné, takzvané „E formě“. Číslo se pak zapisuje například jako 5,46e-8 nebo −8,73E-12. Zápis se používá zejména tam, kde je problematické vysázet exponent.

V programovacích a skriptovacích jazycích se též používá „E-forma“, přičemž u mantisy je případná desetinná čárka nahrazena desetinnou tečkou. E-formu používají i kalkulátory (často mají číslice pro exponent na LCD vyhrazené zvláštní místo).

Příklady a zvláštnosti

Zápis ${\displaystyle 5{,}97\times 10^{24}}$ představuje číslo 5 970 000 000 000 000 000 000 000. To přibližně vyjadřuje hmotnost Země v kilogramech. Čte se: „pět celých devadesát sedm setin krát deset na dvacátou čtvrtou.“ Toto číslo je kladné a je o dvacet čtyři řádů větší než 1.

Zápis ${\displaystyle -1{,}602\times 10^{-19}}$ představuje číslo −0,000 000 000 000 000 000 160 2. To přibližně vyjadřuje elektrický náboj elektronu v coulombech. Čte se: „mínus jedna celá šestset dva tisícin krát deset na mínus devatenáctou.“ Toto číslo je záporné a jeho absolutní velikost je o devatenáct řádů menší (blíže k nule) než 1.

Zápis ${\displaystyle 846\times 10^{0}}$ představuje číslo 846. Tento zápis je nenormalizovaný. Normalizovaný by byl ${\displaystyle 8{,}46\times 10^{2}}$.

Při zapisování čísla se směrodatnou odchylkou se běžně používají dva zápisy.

1) Příkladem prvního může být ${\displaystyle (-3{,}49\pm 0{,}12)\times 10^{5}}$.

2) Příkladem druhého může být ${\displaystyle 8{,}617\,343(15)\times 10^{-5}}$. V tomto případě se směrodatná odchylka týká posledních dvou číslic: ${\displaystyle 0{,}000\,015\times 10^{-5}}$.

A relativní odchylku pak lze spočítat jako poměr směrodatné odchylky vůči původní hodnotě:

${\displaystyle {0{,}000\,015\times 10^{-5} \over 8{,}617\,343\times 10^{-5}}\,{\dot {=}}\,1{,}74\times 10^{-6}=1{,}74\times 10^{-4}\,\%\,.}$

Výjimečně se lze setkat i se zápisem, kde mantisa je určena nějakou konstantou, která může být i iracionální. Například výraz ${\displaystyle 4\pi \times 10^{-7}{\mbox{Hm}}^{-1}}$ je hodnotou permeability vakua. Kombinovaný, nenormovaný tvar se používá, aby při výpočtech nedocházelo ke zbytečným zaokrouhlovacím chybám tam, kde je známa velmi přesná hodnota (například plynoucí z definice).

V zápisu násobení se užívá znak ${\displaystyle \times }$ nebo znak ${\displaystyle \cdot }$ (střední tečka). Znak × lze zpravidla sázet i kombinací kláves Alt 0215, znak · (střední tečka) kombinací kláves Alt 0183. Neužívá se asterisk (hvězdička *). (Spíše než o „vědecký zápis“ jde o pravidla vžitá v matematice a sazbě, resp. grafické úpravě profesionální úrovně.) Striktně platí, že znak × se nikdy nenahrazuje písmenem x (iks).^[2][3] ČSN 01 6910 Úprava dokumentů zpracovaných textovými procesory z roku 2014 se nevztahuje k problematice tohoto článku, viz Otázky a odpovědi k ČSN 01 6910 (2014), s. 17, dostupné v pdf nebo.

Odkazy

Reference

Související články

• plovoucí řádová čárka
• IEEE 754