Věta o obvodovém a středovém úhlu

Věta o obvodovém a středovém úhlu je matematická věta popisující vztah mezi obvodovým a středovým úhlem příslušných jednomu oblouku kružnice.

Znění

Velikost středového úhlu je rovna dvojnásobku velikosti obvodového úhlu příslušného témuž oblouku.

Důkaz

Pro důkaz věty o obvodovém a středovém úhlu se popisují tři případy polohy ostrého obvodového úhlu vůči středu kružnice:

1. Střed kružnice ležící na rameni obvodového úhlu

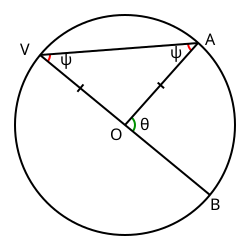
Bod O (střed kružnice k) leží na jednom rameni ostrého obvodového úhlu AVB. Body A, V a B leží na kružnici k, přičemž bod V je vrcholem daného obvodového úhlu a body A a B prochází ramena tohoto úhlu. Trojúhelník VAO je rovnoramenný, protože délky úseček OV a OA (poloměry kružnice) jsou shodné. Z toho vyplývá, že úhly AVO a VAO jsou velikostně také shodné. K velikosti úhlu VOA lze dojít dvěma způsoby:

a) dopočtením vnitřního úhlu trojúhelníku VAO pomocí velikosti obvodového úhlu ψ:

${\displaystyle 180^{\circ }-2\psi }$

b) odečtením úhlu θ od přímého úhlu VOB, kdy θ je středový úhel příslušný menšímu oblouku AB:

${\displaystyle 180^{\circ }-\theta }$

Z čehož vyplývá:

${\displaystyle 180^{\circ }-2\psi =180^{\circ }-\theta }$

${\displaystyle \theta =2\psi }$.

2. Střed kružnice ležící uvnitř obvodového úhlu

Jestliže je bod O vnitřním bodem obvodového úhlu CVD, pak polopřímka VO protíná menší oblouk CD v bodě E a dělí jej na dva oblouky CE a DE. Oblouku DE přísluší obvodový úhel DVE a středový úhel DOE. Podle prvního důkazu je velikost úhlu DOE dvojnásbná velikosti úhlu DVE. Stejně tak lze první důkaz aplikovat pro úhly CVE a COE. Výslednými vztahy jsou rovnice:

${\displaystyle \theta _{1}=2\psi _{1}}$

a

${\displaystyle \theta _{2}=2\psi _{2}}$,

kde ψ₁ a ψ₂ jsou obvodové úhly a θ₁ a θ₂ jsou úhly středové. Sečtením obou rovnic vznikne:

${\displaystyle \theta _{1}+\theta _{2}=2\psi _{1}+2\psi _{2}}$

${\displaystyle \theta _{1}+\theta _{2}=2\left(\psi _{1}+\psi _{2}\right)}$

Součet obvodových úhlů ψ₁ a ψ₂ je roven ψ₀ a součet středových úhlů θ₁ a θ₂ je roven θ₀, z čehož plyne:

${\displaystyle \theta _{0}=2\psi _{0}}$.

3. Střed kružnice ležící vně obvodového úhlu

Jestliže bod O nenáleží obvodovému úhlu DVC, pak polopřímka VO protíná kružnici k v bodě E. K menšímu oblouku ED přísluší obvodový úhel EVD a středový úhel EOD; přitom bod O leží na jednom rameni obvodového úhlu. Podle prvního důkazu je středový úhel EOD opět dvakrát větší než obvodový úhel EVD. Stejně tak je i velikost úhlu EOC dvakrát větší než EVC. Výslednými vztahy jsou rovnice:

${\displaystyle \theta _{1}=2\psi _{1}}$

a

${\displaystyle \theta _{2}=2\psi _{2}}$,

kde ψ₁ a ψ₂ jsou obvodové úhly a θ₁ a θ₂ jsou úhly středové. Odečtením těchto rovnic vychází:

${\displaystyle \theta _{2}-\theta _{1}=2\psi _{2}-2\psi _{1}}$

${\displaystyle \theta _{2}-\theta _{1}=2\left(\psi _{2}-\psi _{1}\right)}$

Rozdíl obvodových úhlů ψ₂ a ψ₁ je roven ψ₀ a rozdíl středových úhlů θ₂ a θ₁ je roven θ₀, z čehož vyplývá:

${\displaystyle \theta _{0}=2\psi _{0}}$.

Větší oblouk a půlkružnice

Pro větší oblouk a půlkružnici je důkaz jednodušší, nastane totiž pouze případ 2.

Důsledky věty

Z věty o obvodovém a středovém úhlu vyplývají tyto důsledky:

• Všechny obvodové úhly příslušné k danému oblouku jsou shodné
• Obvodový úhel příslušný k menšímu oblouku je ostrý
• Obvodový úhel příslušný k většímu oblouku je tupý
• Obvodový úhel příslušný k půlkružnici je pravý - tato věta byla dokázána již Thalétem z Milétu, a je po něm také pojmenována Thaletova věta
• Součet obvodových úhlů příslušných k oběma obloukům AB (menšímu a většímu) je úhel přímý

Reference

V tomto článku byl použit překlad textu z článku Inscribed angle na anglické Wikipedii.

Literatura

• POMYKALOVÁ, Eva. Planimetrie. 5. vyd. Praha: Prometheus, 2015. 208 s. ISBN 978-80-7196-358-5. Kapitola Geometrické útvary v rovině, s. 59–63. 

Související články

• Thaletova věta
• Středový úhel
• Planimetrie