Vnější balistika

Vnější balistika je obor balistiky, která se zabývá chováním vrženého tělesa pouze během letu. V oboru střelných a především hlavňových palných zbraní jde o časový úsek počínající tím, že střela opustí hlaveň až do okamžiku jejího dopadu.[1][2]

Balistická křivka (B), Záměrná (A), Cíl (C), Maximální převýšení balistické křivky (D), Vrchol křivky (E)


Dráha vrženého tělesa

Varianty tvarů balistické křivky

V případě, že by na vržené těleso nepůsobily žádné síly, tak by v souladu s fyzikálními zákony pokračovalo v letu po přímce. Hlavními silami, které v reálném světě ovlivňují jeho dráhu, jsou gravitace a odpor vzduchu. Gravitace působní na projektil silou směřující do středu Země a uděluje mu tedy zrychlení se směrem k zemi. Tím se začne otáčet vektor rychlosti střely k zemi. Pokud by neexistoval odpor vzduchu, těleso by se pohybovalo po parabolické dráze.[2] Odpor vzduchu působí proti směru pohybu, a tím vržené těleso zpomaluje. Tím je dráha vrženého tělesa ovlivněna tak, že její výsledný tvar není parabola, ale je odlišný. Takové dráze říkáme balistická křivka.[2]

Tvar balistické křivky se významně mění podle úhlu výstřelu. Dráha střely je ovlivňována silami, které ji mírně vychylují i v příčném směru. Balistická křivka je tedy ve skutečnosti prostorová. Na obrázku je znázorněn její průmět do svislé roviny.

Balistika a palné zbraně

Podrobně je balistika rozpracovávána především v souvislosti se střelbou z palných zbraní. V dalším textu jsou uváděny především poznatky publikované v materiálech týkající se střelecké balistiky a soustředí se na výpočty dráhy jednotné střely stabilizované její rotací okolo její podélné osy. Ve skutečnosti je při střelbě první okamžik od chvíle, kdy střela opustí hlaveň cca do vzdálenosti 20 ráží od konce hlavně, předmětem zkoumání přechodové balistiky. Působení vlivů zkoumaných v rámci přechodové balistiky bývá pro zjednodušení zanedbáno, respektive je zahrnuto do vnější balistiky takovým způsobem, aby bylo eliminováno. [1]

Prvky dráhy střely

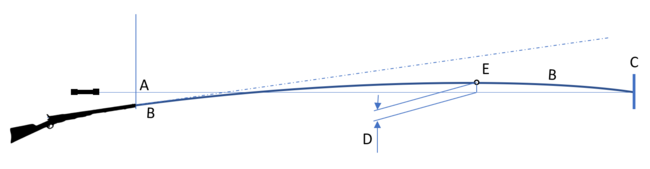
Pro bližší popis dráhy střely, tedy balistické křivky (na obrázku označeno B), jsou definovány následující pojmy:

  • Náměrná – přímka procházející osou hlavně před výstřelem
  • Výstřelná - přímka procházející osou hlavně v okamžiku výstřelu
  • Záměrná - přímka procházející body hledí – muška – záměrný bod (A)
  • Úroveň ústí – vodorovná rovina procházející středem ústí hlavně
  • Dálka střelby – vzdálenost od ústí hlavně k cíli (cíl označen C)
  • Bod doletu(dopadu) – průsečík dráhy střely s úrovní ústí (s povrchem)
  • Dostřel - vzdálenost od ústí hlavně k bodu doletu(dopadu)
  • Úhel výstřelu - úhel mezi výstřelnou a úrovní ústí.
  • Vrchol dráhy střely – nejvyšší bod balistické křivky (E)
  • Převýšení dráhy střely – okamžitá výška střely nad/pod záměrnou. Maximum dosahuje ve vrcholu dráhy střely (D)

Stabilizace střely

Pro stabilizaci střely se používá několik způsobů:[1]

  • Gyroskopická stabilizace
  • Stabilizace křídly
  • Stabilizace čelní hranou

Stabilizace jednotné střely je u hlavňových zbraní nejčastěji prováděna gyroskopicky, tedy rotací okolo podélné osy střely, která je před výstřelem totožná s osou hlavně. Tato stabilizace ovlivňuje také ostatní síly působící na střelu. Navíc může dojít v důsledku nesprávné laborace střely a dalších konstrukčních vlivů k tomu, že střela není stabilizovaná optimálně. Lze identifikovat tři základní stupně stabilizace střely.[2]

  • Optimálně stabilizovaná střela – v tomto případě sleduje podélná osa střely po celou dráhu letu vektor rychlosti střely a dráha střely je nejdelší.
  • Přestabilizovaná střela – podélná osa střely je při letu střely stále ve směru výstřelné. Odpor vzduchu tím roste a dráha střely se zkracuje.
  • Podstabilizovaná střela – ztrácí stabilitu ještě během letu. Střela se začne za letu převracet kolem osy kolmé na svou podélnou osu a směr letu. Dráha střely je v tomto případě nejkratší.

Síly působící na střelu

Při střelbě na velmi krátkou vzdálenost a plochou dráhu letu může i kriminalistická balistika počítat se zjednodušením dráhy střely na přímku. [2] Naopak při střelbě na dlouhou vzdálenost se uplatňuje výrazněji i vliv dalších sil.

Rozdělení sil působících na střelu

  • základní[1]
    • tíže
    • odpor vzduchu
      • čelní odpor
      • podtlak na spodní části střely
      • vztlak[2]
      • odpor tření
  • doplňkové[1]
    • pravidelné
      • Magnusova síla
      • povrchové tření
      • Coriolisova síla
    • nepravidelné
      • aerodynamické síly

Tíže

Zemská tíže je ovlivněna přitažlivostí Země a odstředivým zrychlením. Pro výpočet je gravitační síla reprezentována gravitačním zrychlením. Pro výpočty vnější balistiky se v České republice používá normální tíhové zrychlení gn = 9,806 65. Gravitační zrychlení se mění dle zeměpisné šířky a nadmořské výšky.

Odpor vzduchu

Odpor vzduchu není konstantní. Pro pomalé střely je odpor vzduchu nejmenší a jejich balistická dráha letu se blíží parabole. S rostoucí rychlostí střely roste také hodnota odporu vzduchu. Lze vyjádřit funkční závislost odporu vzduchu na rychlosti střely. Při malé rychlosti střely je tato funkce lineární. Pokud se rychlost střely blíží zvuku, je funkce úměrná třetí mocnině rychlosti střely.[2]

Funkce odporu vzduchu závisí na tvaru střely. Často bývá funkce odporu vzduchu vyjádřena pro etalonovou střelu. Pro různé tvary střel existují tvarové koeficienty. Při výpočtu se hodnota funkce daná pro etalonovou střelu násobí koeficientem konkrétní střely. Působiště síly odporu vzduchu je u střel stabilizovaných rotací za těžištěm střely a u střel se šípovou stabilizací před těžištěm. Odpor vzduchu má několik složek. Jde o čelní odpor, vztlak, odpor sání způsobený podtlakem na zadní částí střely a třecí odpor. Odpor vzduchu ovlivňují následující fyzikální vlivy:[1]

  • Vnitřní tření prostředí
  • Tvoření vírů při obtékání střely
  • Vznik balistické vlny (nadzvukové rychlosti střel)

Magnusova síla

Při rotaci střely na jejím povrchu ulpívá a spolu s ní rotuje také tenká vrstva vzduchu. V místě opačného pohybu této vrstvy a okolního vzduchu vzniká zhuštění vzduchu a na opačné straně zředění. Tím vzniká síla ve směru od zhuštění ke zředění. Magnusova síla je výraznější při silnějším příčném větru. Magnusova síla vychyluje střelu proti směru rotační gyroskopické stabilizace.

Povrchové tření

Tato síla je spojena s ulpívající vrstvou vzduchu. Viz popis Magnusovy síly. Tato vrstva vytváří odpor, který působí proti rychlosti otáčení střely kolem její podélné osy.

Coriolisova síla

Soustava souřadnic, která se používá k určení polohy bodu vystřelení a letícího tělesa, je systém poledníků a rovnoběžek, které rotují spolu se zemí. Pro malé vrhy je tato rotace zanedbatelná, ale pří delších letech tělesa využívajících např. dělostřelectvo a balistické rakety, to je důležitý faktor. Když se nanese rovná trajektorie na systém souřadnic, bude se jevit jako křivka. Pokud chceme vzít v potaz rotaci systému, musíme zavést odstředivou sílu a Coriolisovu sílu. Pokud do rovnice pohybu zavedeme Coriolisovu sílu, předpokládaná dráha letu bude respektovat otáčení systému a zakřiví se.

Balistické charakteristiky střely

Balistický koeficient

Vyjadřuje balistické vlastnosti střely. Je přímo úměrný koeficientu tvaru střely, druhé mocnině vnějšího průměru střely a nepřímo úměrný její hmotnosti.

Průřezové zatížení

Vyjadřuje dostřel, zakřivení dráhy a dobu letu. Vyšší průřezové zatížení konkrétního náboje znamená delší dostřel a plošší dráhu letu střely.

Poměrná hmotnost střely

Jde o parametr daný konstrukcí střely. Jde o poměr hmotnosti střely a třetí mocniny její ráže.

Dostřel

Praktický výpočet dostřelu s uvážením všech vlivů je komplikovaný. Dostřel je dán nejen vlastnostmi střely, ale celým systémem do kterého patří jak náboj, tak hlaveň. S danou soustavou lze dostřel ovlivnit úhlem náměru, respektive úhlem výstřelu. Teoreticky je maximální dostřel při úhlu výstřelu 45°, což ale neplatí při reálných podmínkách, kdy působí na střelu účinky prostředí. V praxi roste vodorovný dostřel do náměru cca do 30°. Konkrétní úhel největšího dostřelu je specifický pro daný systém náboj - hlaveň a například u ručních palných zbraní se pohybuje obvykle mezi náměrem 25° a 45°.[1]

Dostřel lze prodloužit výběrem střeliva:

  • Vyšší úsťová rychlost;
  • Lepší vlastnosti výmetné náplně;
  • Zmenšení odporu prostředí na střelu (např. vhodný tvar střely, vyšší průřezové zatížení).

Přibližný maximální dostřel některých nábojů:

  • .22LR 1700 m
  • 7,62 Tokarev 1800 m
  • 9mm Luger 1700 m

Odkazy

Reference

  1. ↑ a b c d e f g Caras, J. : Střelivo do ručních palných zbraní, ARS-ARM Praha (1995) , ISBN 80-900833-8-2
  2. ↑ a b c d e f g Planka, B. : Kriminalistická balistika, Vydavatelství a nakladatelství Pavel Čeněk, Plzeň 2010, ISBN 978-80-7380-036-9

Související články

Literatura

  • Kneubuehl, B.: Balistika: střely, přesnost střelby, účinek. Praha: Naše vojsko. 2004. ISBN 80-206-0749-8
  • Komenda, J. a kolektiv: Balistika. Skripta. VA v Brně, 2004
  • PÍRKO, Zdeněk. Co jsou balistika a zvukoměřičství?. 1. vyd. Praha: Jednota českých matematiků a fysiků, 1944. 34 s. 

Externí odkazy

Média použitá na této stránce

Ballistic curve.png
Autor: Oldřich Lebeda 2, Licence: CC BY-SA 3.0
Na obrázku je sada křivek modelujících setrvačný pohyb tělesa ve svislém gravitačním poli při uvažování odporu prostředí. Křivky odpovídají drahám stejných těles o stejně velké počáteční rychlosti vypuštěných pod různými náměry. Na křivkách jsou vyznačeny body označující stejně dlouhé časové úseky.
Ballistic curve with gun.png
Autor: SvaRoM, Licence: CC BY-SA 4.0
Chart containing - ballistic curve, sight line, target, rifle