Zlatý řez

Jako zlatý řez (latinsky sectio aurea) se označuje poměr o hodnotě přibližně 1,618 : 1 (resp. 1 : 0,618). V umění a fotografii je pokládán za ideální proporci mezi různými délkami. Zlatý řez vznikne rozdělením úsečky na dvě části tak, že poměr větší části k menší je stejný jako poměr celé úsečky k větší části. Hodnota tohoto poměru je iracionální číslo
Již nejméně od renesance využívají zlatý řez umělci ve svých dílech, zejména ve formě tzv. zlatého obdélníku, ve kterém se zlatý řez vyskytuje jako poměr stran. Zlatý řez prý totiž působí esteticky příznivým dojmem; poměr zlatého řezu lze také pozorovat v přírodě.[1]
Značení písmenem φ začal na počátku 20. století používat Mark Barr, přičemž je zvolil na počest řeckého sochaře Feidia (cca 490–430 př. n. l.), který podle historiků ve svých dílech zlatý řez hojně využíval. Občas se používá také označení τ z řeckého tome = řez.
| „ | Geometrie má dva poklady: Pythagorovu větu a zlatý řez. První má cenu zlata, druhý připomíná spíše drahocenný kámen. | “ |
| — Johannes Kepler | ||
Vlastnosti

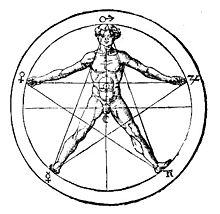
Zlatý řez má mnoho zajímavých vlastností. Například se vyskytuje v pravidelném pětiúhelníku nebo je to limita poměru mezi dvěma následujícími členy Fibonacciho posloupnosti. Pentagram (penta – pět, grame – čára) je pěticípá hvězda nakreslená jedním tahem, která má sice chybu na kráse, neboť ji křižují čáry a oddělují ramena od středu, ale vzdálenosti mezi vrcholy jsou v poměru zlatého řezu. Pentagram měli Řekové ve velké úctě, neboť názorně představoval to, co neuměli vyjádřit číselným poměrem. Zákonitost, která se v pentagramu ukrývala, z něj učinila tajemný symbol dokonalosti vesmíru.[2]
Obdélník, jehož poměr stran odpovídá zlatému řezu, lze rozdělit na čtverec a obdélník, jehož poměr stran opět odpovídá zlatému řezu.
Výpočet
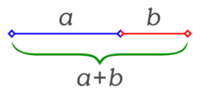
Pokud části úsečky označíme jako a , musí platit
- , přičemž .
To znamená, že , což po dosazení do první rovnice dává
- .
Úpravou této rovnice se získá kvadratická rovnice
- ,
jejímž kladným kořenem (záporný zde nemá smysl) je
- .
Převrácený poměr
Převrácená hodnota zlatého řezu je rovna také výrazu , jinými slovy, u čísla i je shodná část za desetinnou čárkou. Tato unikátní vlastnost vede na stejnou kvadratickou rovnici jako výše, takže z ní lze hodnotu zlatého řezu rovněž vypočítat.
Zápis zlatého řezu v desítkové soustavě
1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362 1076738937 6455606060 5921658946 6759551900 4005559089 ...
Další vzorce
1. 1 2. 1,4142135623731 3. 1,5537739740300 4. 1,5980531824786 5. 1,6118477541253 6. 1,6161212065081 7. 1,6174427985274 8. 1,6178512906967 9. 1,6179775309347 10. 1,6180165422315 11. 1,6180285974702 12. 1,6180323227520 13. 1,6180334739282 14. 1,6180338296612 15. 1,6180339395888 16. 1,6180339735583 17. 1,6180339840554 18. 1,6180339872992 19. 1,6180339883016 20. 1,6180339886114 21. 1,6180339887071 22. 1,6180339887367 23. 1,6180339887458 24. 1,6180339887486 25. 1,6180339887495 26. 1,6180339887498
Číslo lze vyjádřit pomocí řetězového zlomku:
Pokud vezmeme libovolné číslo , pak iterativní posloupnost konverguje ke zlatému řezu.
i abs err Pi Qi ai -- -------- ---------- ---------- ------------------ 0 6.2E-01 1 / 1 = 1.000000000000000 1 -3.8E-01 2 / 1 = 2.000000000000000 2 1.2E-01 3 / 2 = 1.500000000000000 3 -4.9E-02 5 / 3 = 1.666666666666667 4 1.8E-02 8 / 5 = 1.600000000000000 5 -7.0E-03 13 / 8 = 1.625000000000000 6 2.6E-03 21 / 13 = 1.615384615384615 7 -1.0E-03 34 / 21 = 1.619047619047619 8 3.9E-04 55 / 34 = 1.617647058823529 9 -1.5E-04 89 / 55 = 1.618181818181818 10 5.6E-05 144 / 89 = 1.617977528089888 11 -2.2E-05 233 / 144 = 1.618055555555556 12 8.2E-06 377 / 233 = 1.618025751072961 13 -3.1E-06 610 / 377 = 1.618037135278515 14 1.2E-06 987 / 610 = 1.618032786885246 15 -4.6E-07 1597 / 987 = 1.618034447821682 16 1.8E-07 2584 / 1597 = 1.618033813400125 17 -6.7E-08 4181 / 2584 = 1.618034055727554 18 2.6E-08 6765 / 4181 = 1.618033963166706 19 -9.8E-09 10946 / 6765 = 1.618033998521803 20 3.7E-09 17711 / 10946 = 1.618033985017358 21 -1.4E-09 28657 / 17711 = 1.618033990175597 22 5.4E-10 46368 / 28657 = 1.618033988205325 23 -2.1E-10 75025 / 46368 = 1.618033988957902 24 7.9E-11 121393 / 75025 = 1.618033988670443 25 -3.0E-11 196418 / 121393 = 1.618033988780243 26 1.2E-11 317811 / 196418 = 1.618033988738303 27 -4.4E-12 514229 / 317811 = 1.618033988754322 28 1.7E-12 832040 / 514229 = 1.618033988748204 29 -6.5E-13 1346269 / 832040 = 1.618033988750541 30 2.5E-13 2178309 / 1346269 = 1.618033988749648
Pozn.: Pi = Pi-1 + Qi-1; ai = Pi / Qi; viz též Fibonacciho posloupnost.
Konstrukce zlatého řezu
Zlatý řez je jakožto kvadratická iracionalita euklidovsky konstruovatelným číslem (pomocí kružítka a pravítka).

- Bodem B úsečky AB o délce a sestrojíme kolmici BC o délce ½ a.
- Spojíme bod A s bodem C.
- Sestrojíme kružnici se středem C a poloměrem ½ a.
- Průnikem kružnice a úsečky AC je bod D.
- Naneseme úsečku AD na úsečku AB z bodu A.
- Bod E, který dostaneme, rozdělí úsečku AB zlatým řezem.
Alternativní konstrukce
- Mějme čtverec ABCD a bod A', který stranu AB rozděluje na polovinu. Uvažujme i polopřímku AB.
- Z bodu A' sestrojíme kružnici tak, aby procházela bodem C. Kružnice nám protne polopřímku v bodě E.
- Vzdálenosti AE a AD jsou v poměru zlatého řezu.
- Jako bod F si označíme koncový bod vektoru AD aplikovaného z bodu E.
- Obdélník AEFD má strany v poměru zlatého řezu, stejně jako obdélník BEFC.
Zlatý řez v přírodě
Zlatý řez se vyskytuje v přírodě ve formě Fibonacciho posloupnosti. Listy rostlin, pokud vyrůstají jednotlivě, jsou na větvičkách rozloženy tak, že každý list vyrůstá nad předchozím listem více či méně posunut o určitý úhel. V dolní části stonku jsou listy starší a větší, u vrcholu mladší a menší. Všechny listy jsou stejnoměrně osvětlovány Sluncem, menší nestíní větším, které mají delší řapíky. Dalším projevem zlatého řezu je uspořádání semen slunečnice nebo smrkové šišky, ve kterých jsou šupiny rozmístěny jako spirála, nebo točité schody. Toto rozmístění je také velice dobře vidět u ananasu. Dalším projevem zlatého řezu v přírodě je logaritmická spirála, která nemění tvar a roste stejně do délky i do šířky. Jejím projevem je růst neživých částí živého tvora. Mohou to být vlasy, nehty, zobáky, zuby, rohy, parohy nebo schránky měkkýšů. Čím více se její zakřivení liší od zakřivení kružnice, tím méně připomíná spirálu. Mírně ohnutý sloní kel i hustě točená ulita plže jsou v tomto ohledu příbuzné. Turovitým kopytníkům, mezi které patří i náš hovězí dobytek a ovce, rostou rohy do spirály. Nebývá to vždy na první pohled zřetelné, neboť obyčejně jsou jen částí jednoho závitu spirály, ale některé jsou přímo ukázkou prostorové logaritmické spirály, např. africký kudu. Spirálu najdeme v klu slona nebo zubu narvala. Narval má zubů velmi málo, pouze v horní čelisti. Samci jeden z těchto zubů naroste do obrovských rozměrů. Je to vždy levý zub a na povrchu je spirálovitá struktura. Je také rozšířen mýtus,[3] že na lidském těle lze zlatý řez pozorovat tehdy, jestliže se výška postavy (od temene hlavy) dělí vzdáleností pupku od země.
Schránka hlavonožce loděnky je ilustrací logaritmické spirály. Nejlépe se o tom přesvědčíme na průřezu ulity. Přepážky, které ji rozdělují na komůrky, svědčí o tom, jak loděnka rostla. Logaritmická spirála je příznačná pro neživé části živého organismu ulity plžů. Také hmyz se ke světlu blíží po logaritmické spirále. Pohybuje se tak, aby světlo viděl stále pod stejným úhlem.[4]
- Samičí šiška smrku ztepilého
- Květ slunečnice
- Plod ananasu
- (c) Andrew Butko, CC BY-SA 3.0Schránka plže
- Hlavonožec Nautilus
- Lebka narvala s dvěma zuby („kly“)
Zlatý řez v umění
Malíři 1830–1870 Barbizonské školy kompozici zlatého řezu také uplatňovali:
- 1802–1868 Camille Flers
- 1807–1876 Narcisse Virgile Diaz
- 1808–1893 Jules Jacques Veyrassat
- 1810–1865 Constant Troyon
- 1812–1867 Théodore Rousseau
- 1813–1894 Charles Emile Jacque
- 1817–1878 Charles Francois Daubigny
- 1829–1900 Paul Desire Trouillebert
- 1836–1897 Homer Dodge Martin
Podobně jako v umění, pracuje se hojně se zlatým řezem i v dalších disciplínách, kde je důležité estetické působení na diváka či pozorovatele – např. v architektuře, designu, fotografii atd. Druhý hlavní princip, využívaný často v duchu klasické estetiky, je princip symetrie.
Odkazy
Reference
- ↑ Ing. arch. Dušan Řezáč: Le Corbusier – MODULOR, archiweb.cz, 2007-09-26. Navštíveno 2008-03-24.
- ↑ http://www.volny.cz/zlaty.rez/diplomka8.html
- ↑ The Myth That Will Not Go Away [online]. [cit. 2020-02-01]. Dostupné v archivu pořízeném dne 2022-02-25.
- ↑ http://www.volny.cz/zlaty.rez/diplomka6.html
Literatura
- LIVIO, Mario. Zlatý řez: příběh fí, nejpodivuhodnějšího čísla na světě. Praha : Argo a Dokořán, 2006.
Související články
- Zlatý úhel
- Fraktál
- Historie kompozice obrazů
- Zlatý prostorový úhel
- Section d'Or – umělecká skupina
- Fibonacciho posloupnost
Externí odkazy
 Obrázky, zvuky či videa k tématu zlatý řez na Wikimedia Commons
Obrázky, zvuky či videa k tématu zlatý řez na Wikimedia Commons  Téma Zlatý řez ve Wikicitátech
Téma Zlatý řez ve Wikicitátech Slovníkové heslo zlatý řez ve Wikislovníku
Slovníkové heslo zlatý řez ve Wikislovníku Výukový kurs Zlatý řez ve Wikiverzitě
Výukový kurs Zlatý řez ve Wikiverzitě- Zlatý řez v České terminologické databázi knihovnictví a informační vědy (TDKIV)
- Diplomová práce na téma Zlatý řez
- Zlatý řez v encyklopedii MathWorld (anglicky)
- Číslice zlatého řezu, oeis.org, On-Line Encyclopedia of Integer Sequences
- Fibonacci and the Golden Mean
- Šárka GERGELITSOVÁ, Tomáš HOLAN: The Golden Ratio Determined Using a Ruler and Compass, Matfyzpress, Praha 2015
Média použitá na této stránce
Autor: Agnieszka Kwiecień (Nova), Licence: CC BY-SA 3.0
Picea abies cone and seeds, woods near Wrocław, Poland.
Image of a human body in a circumscribed pentagram, from chapter 27 of book 2 of Heinrich Cornelius Agrippa's Libri tres de occulta philosophia ("three books of occult philosophy"). Symbols of the sun and moon are in center, while the other five classical "planets" are around the edge.
Autor: Jan Hamsik, Licence: CC BY 3.0
Kompozice obrazu
Zlatý řez
Autor: soebe, Licence: CC BY-SA 3.0
Narwhal (Monodon monoceros) skull with two tusks, as seen in the Zoological Museum in Hamburg, Germany; photographed in September of 2004 by Sönke Behrends. The picture was taken in the Zoological Museum in Hamburg. The object is behind protective glas, which causes some reflections. Flash was switched off for that matter. The worst reflections were edited. The skull was brought to Hamburg in 1684, and provably originates from a female animal. The German description provided by the museum translates to:
“The right tooth can also grow into a tusk in very rare cases, as proven by 12 skulls collected by various museums during the past 300 years.
These skulls show, that the second tooth can be developed to a very different degree, and even -- unexpectedly -- the spiralling direction of growth is towards the left and not towards the right mirroring the other half.
All these skulls with two tusks originate from male animals; however, the skull in Hamburg is provably that of a female. It is thus unique.”
(c) Andrew Butko, CC BY-SA 3.0
A shel of the land snail Eobania vermiculata, from Sevastopol, Crimea, Ukraine
1-The golden ratio (phi) represented as a line divided into two segments a and b, such that the entire line is to the longer a segment as the a segment is to the shorter b segment: φ = (a+b) : a = a : b.
Autor:
Pentagramm. Farbig eingezeichnet sind 3 Streckenpaare, die im Verhältnis des Goldenen Schnittes stehen. Die markierten Punkte und die Hilfslinie CC' werden für den Beweis benötigt, dass der Goldene Schnitt vorliegt.

































